最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入: ["flower","flow","flight"]输出: "fl"
示例 2:
输入: ["dog","racecar","car"]输出: ""解释: 输入不存在公共前缀。
说明:
所有输入只包含小写字母 a-z。
解题思路
水平扫描法
思路:
首先,我们将秒数一种查找一组字符串的最长公共前缀 LCP(S1, ..., Sn) 的简单方法。
我们将会用到这样的结论:
LCP(S1, ..., Sn) = LCP(LCP(LCP(S1, S2), S3), ..., Sn)
算法:
为了运用这种思想,算法要依次遍历字符串 [S1, ..., Sn],当遍历到第 i 个字符串的时候,找到最长公共前缀 LCP(S1, ..., Si)。当 LCP(S1, ..., Si) 是一个空串的时候,算法就结束了。否则,在执行了 n 次遍历之后,算法就会返回最终答案 LCP(S1, ..., Sn)。
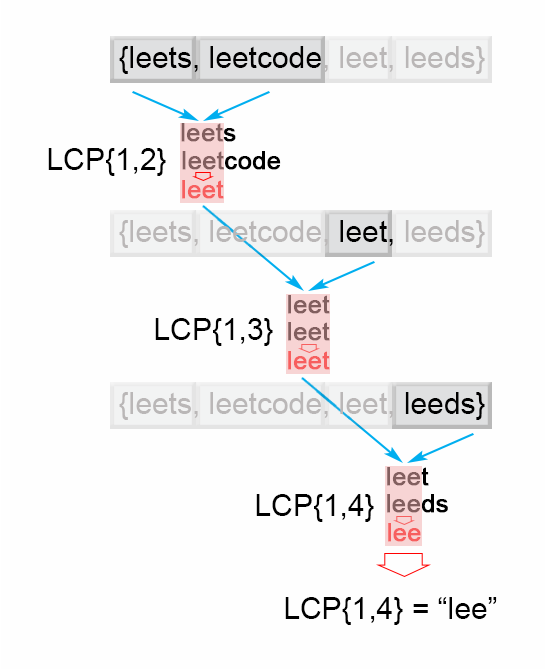
- 取第一个字符串作为比较方,然后遍历判断剩余
n个字符串 - 第
n个字符串和比较方比较相同位置的index的字符是否一致
var longestCommonPrefix = function(strs) {if (strs.length === 0) return '';let prefix = strs[0];for (let i = 0; i < strs.length; i++) {while (strs[i].indexOf(prefix) !== 0) {// 遍历到对应数组成员检索前缀字符串为非 0 时// 表示当前前缀字符串并不匹配当前数组成员的前缀// 因此去除前缀字符串末位字符后继续匹配prefix = prefix.substring(0, prefix.length - 1);// 当前缀为空时则表示无公共前缀if (prefix === '') return '';}}return prefix;};
复杂度分析
- 时间复杂度:
O(S),S 是所有字符串字符数量的总和。最坏的情况下,n个字符串都是相同的,算法会将 S1 与其他字符串[S2, ..., Sn]都做一次比较,这样就会进行 S 次字符比较,其中 S 是输入数据中所有字符数量。 - 空间复杂度:
O(1),我们只需要使用常数级别的额外空间
水平扫描
想象数组的末尾有一个非常短的字符串,使用上述方法依旧会进行 S 次比较。优化这类情况的一种方法就是 水平扫描。我们从前往后枚举字符串的每一列,先比较每个字符串相同列上的字符(即不同字符串相同下标的字符)然后再进行对下一列的比较。
var longestCommonPrefix = function(strs) {if (strs === null || strs.length === 0) return '';for (let i = 0; i < strs[0].length; i++) {const char = strs[0].charAt(i);for (let j = 1; j < strs..length; j++) {if (i === strs[j].length || strs[j].charAt(i) !== char) {return strs[0].substring(0, i);}}}return strs[0];}
复杂度分析
- 时间复杂度:
O(S),S 是所有字符串中字符数的总和。最坏情况下,输入数据为 n 个长度为 m 的相同字符串,算法会进行S = m * n次比较。可以看到最坏情况下,本算法的效率与算法一相同,但是最好的情况下,算法只需要进行n * minLen次比较,其中minLen是数组中最短字符串的长度 - 空间复杂度:
O(1),我们只需要使用常数级别的额外空间
分治
分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。
这道题就是一个典型的分治策略问题:
- 问题:求多个字符串的最长公共前缀
- 分解成多个相似的子问题:求两个字符串的最长公共前缀
- 子问题可以简单求解:两个字符的最长公共前缀求解很简单
- 原问题的解为子问题解的合并:多个字符串的最长公共前缀为两两字符串的最长公共前缀的最长公共前缀,我们可以归并比较两最长公共前缀字符串的最长公共前缀,直到最后归并比较成一个,则为字符串数组的最长公共前缀:
LCP(S1, S2, ..., Sn) = LCP(LCP(S1, Sk), LCP(Sk+1, Sn))
以 ["abc", "abcd", "ab", "ac"] 为例:
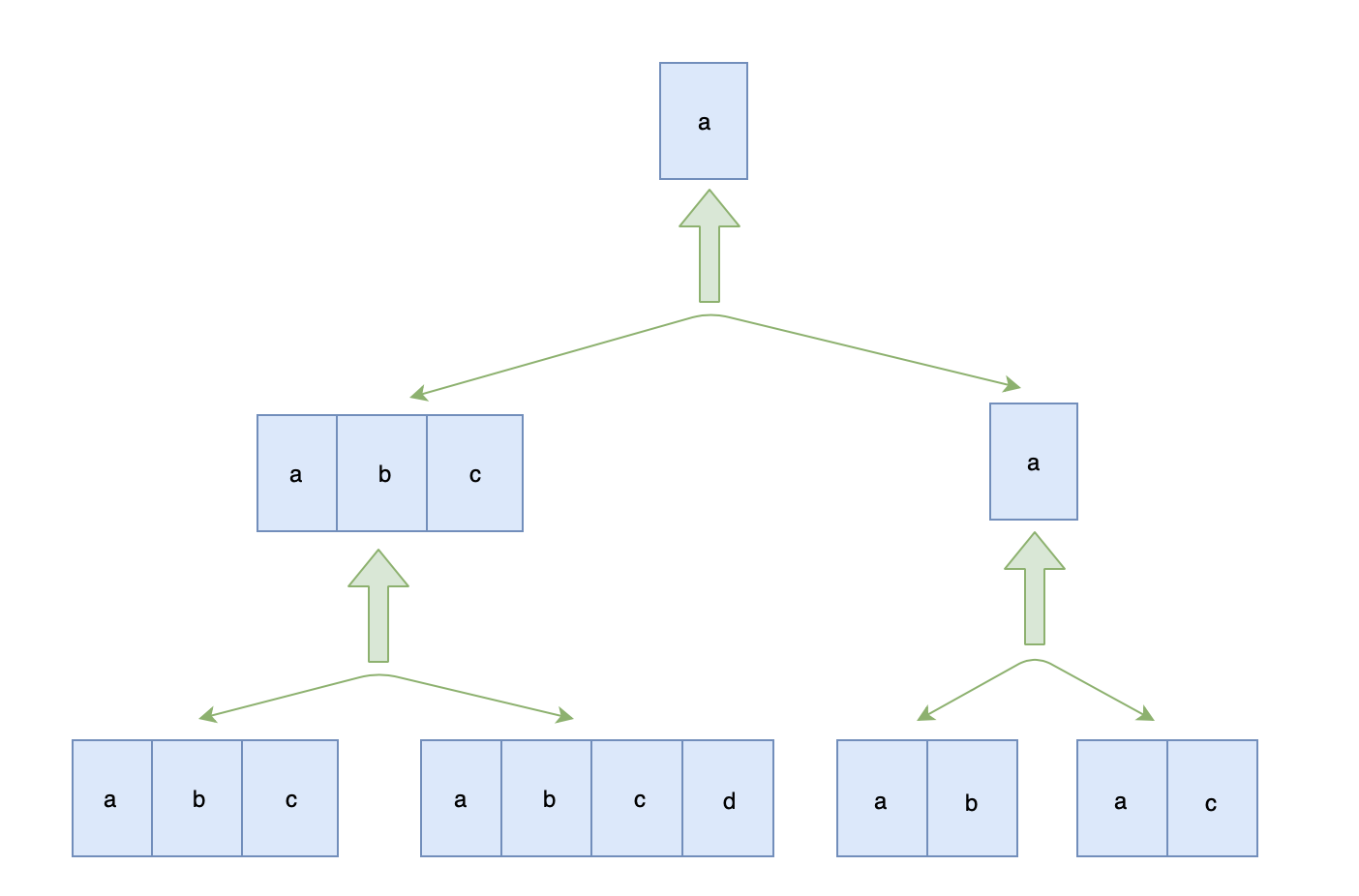
var longestCommonPrefix = function(strs) {if (strs === null || strs.length === 0) return '';return partition(strs);};// 若分裂后的两个数组长度不为 1,则继续分裂// 直到分裂后的数组长度为 1// 然后比较获取最长公共前缀var partition = function(strs) {const len = strs.length;if (len === 1) return strs[0];let mid = Math.floor(len / 2),left = partition(strs.slice(0, mid)),right = partition(strs.slice(mid, length));return commonPrefix(left, right);};// 求 str1 与 str2 的最长公共前缀var commonPrefix = function(str1, str2) {let i = 0;for (; i < str1.length && i < str2.length; i++) {if (str1.charAt(i) !== str2.charAt(i)) {break;}}return str1.substring(0, i);};
复杂度分析
最坏情况下,我们有 n 个长度为 m 的相同字符串。
- 时间复杂度:
O(S),S 是所有字符串中字符数量的总和,S = m * n,时间复杂度的递推式为T(n) = 2 * T(n / 2) + O(m),化简后可知其就是O(S)。最好情况下,算法会进行minLen * n次比较,其中minLen是数组中最短字符串的长度 - 空间复杂度:
O(m * log(n)),内存开支主要是递归过程中使用的栈空间所消耗的,一共会进行log(n)次递归,每次需要m的空间存储返回结果,所以空间复杂度为O(m * log(n))。