最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x)—— 将元素 x 推入栈中。pop()—— 删除栈顶的元素。top()—— 获取栈顶元素。getMin()—— 检索栈中的最小元素。
示例:
输入:["MinStack","push","push","push","getMin","pop","top","getMin"][[],[-2],[0],[-3],[],[],[],[]]输出:[null,null,null,null,-3,null,0,-2]解释:MinStack minStack = new MinStack();minStack.push(-2);minStack.push(0);minStack.push(-3);minStack.getMin(); --> 返回 -3.minStack.pop();minStack.top(); --> 返回 0.minStack.getMin(); --> 返回 -2.
提示:
pop、top和getMin操作总是在 非空栈 上调用。
解题思路
辅助栈
思路
要做出这道题目,首先要理解栈结构先进后出的性质。
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。
那么,我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,我们就可以直接返回存储的最小值 m。
算法
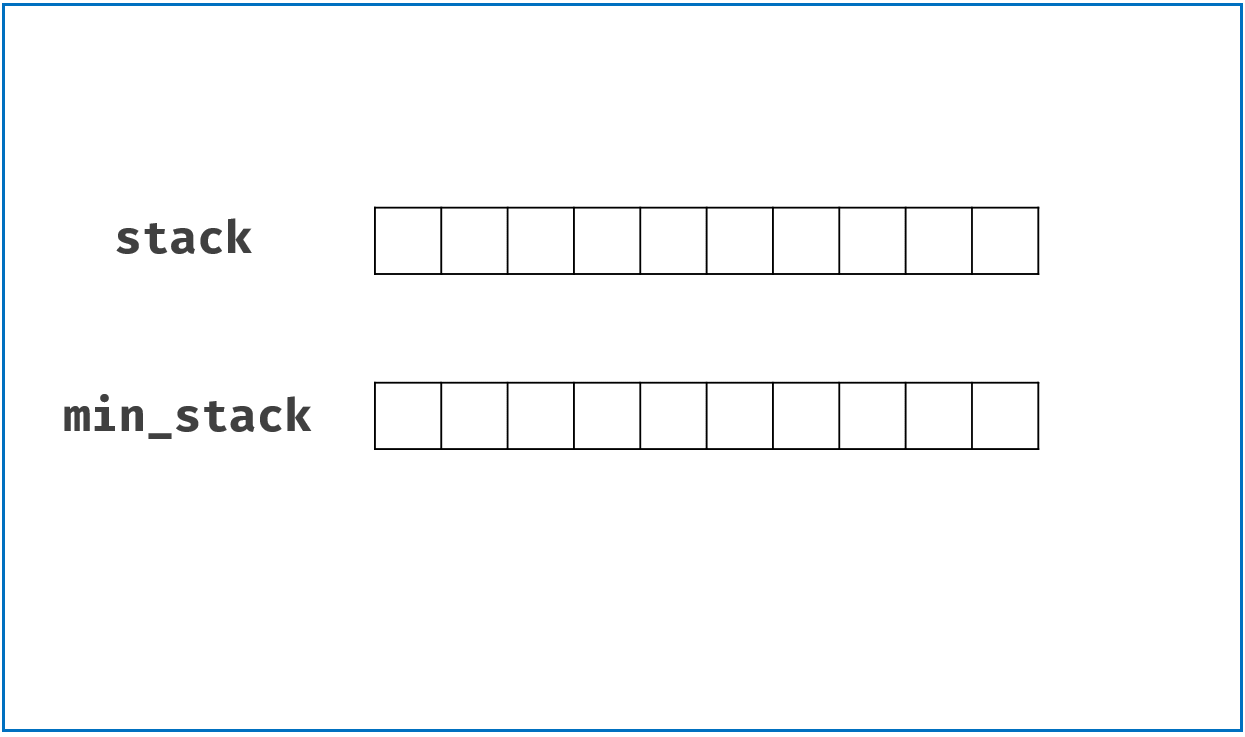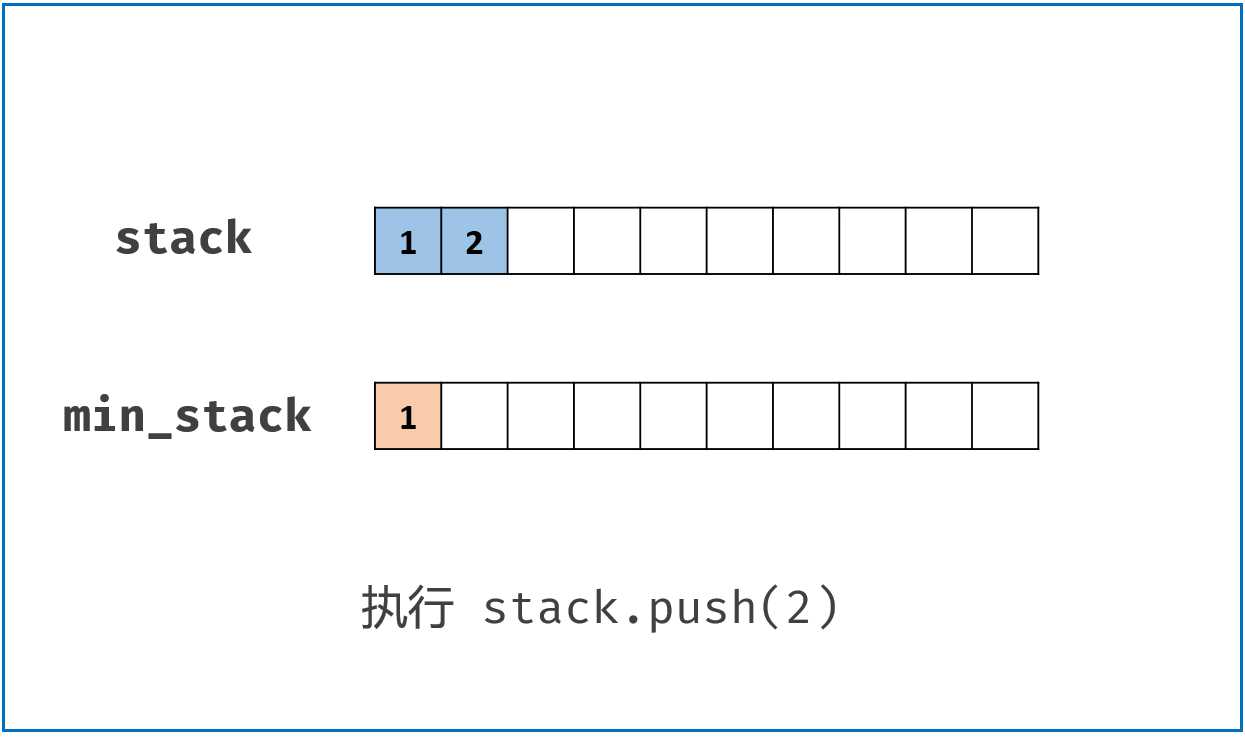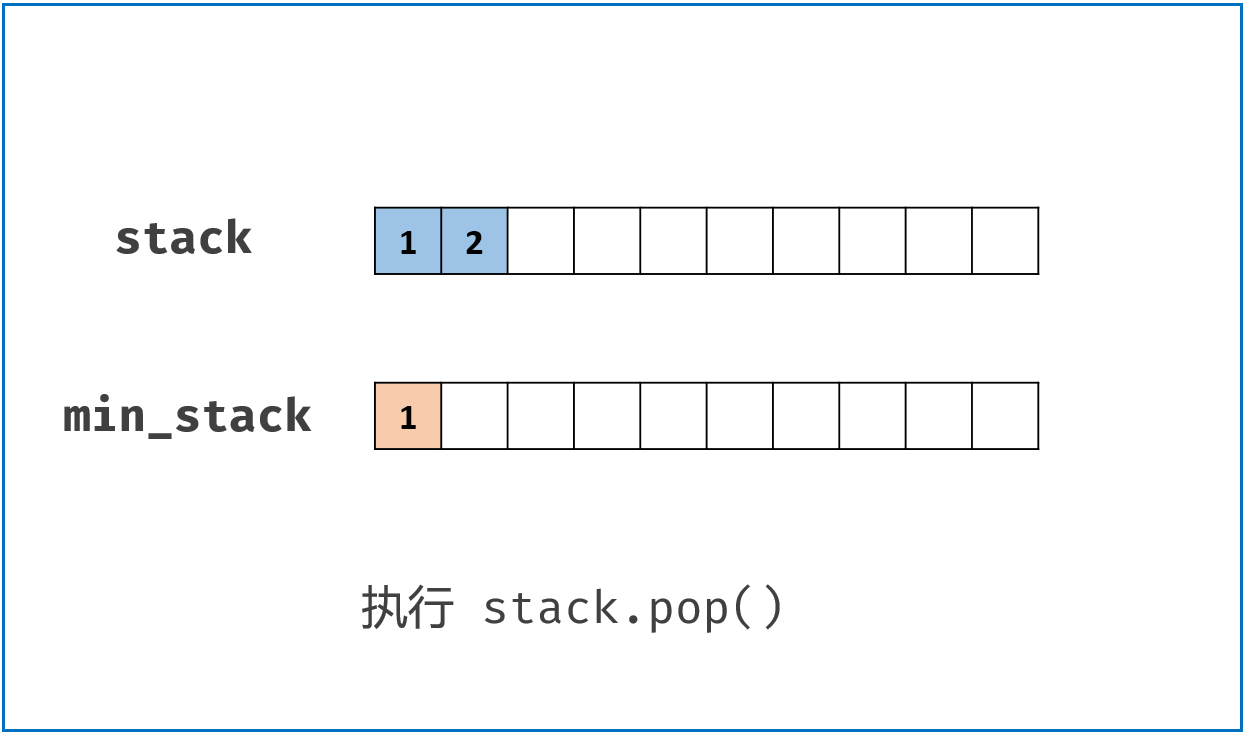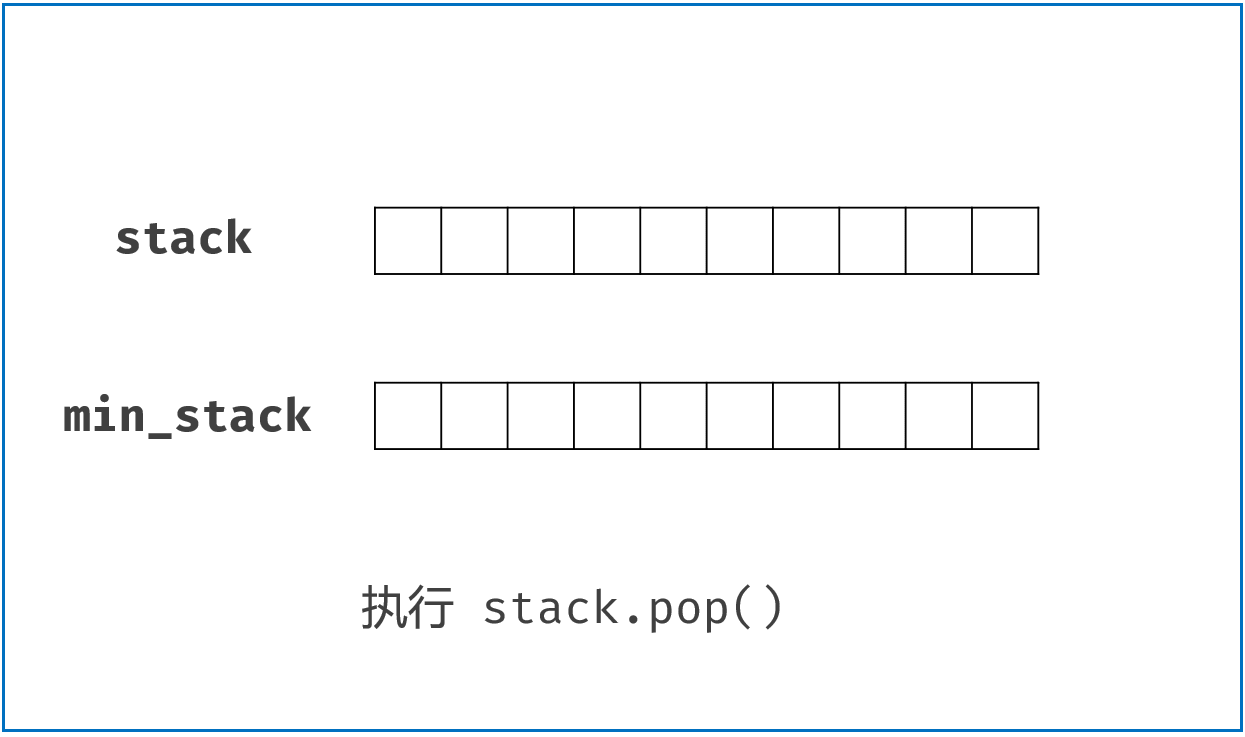
按照上面的思路,我们只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
- 当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
- 当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
- 在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
const MinStack = function() {this.stack = [];this.minStack = [Infinity];};MinStack.prototype.push = function(value) {this, stack.push(value);this.minStack.push(Math.min(this.minStack[this.minStack.length - 1], value));};MinStack.prototype.pop = function() {this.stack.pop();this.minStack.pop();};MinStack.prototype.top = function() {return this.stack[this.stack.length - 1];};MinStack.prototype.getMin = function() {return this.minStack[this.minStack.length - 1];};
复杂度分析
- 时间复杂度:
O(1),压栈、出栈,获取最小值的时间复杂度都为O(1) - 空间复杂度:
O(N),包含 N 个元素辅助栈占用线性大小的额外空间