环形链表 II

给定一个链表，返回链表开始入环的第一个节点。  如果链表无环，则返回  null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

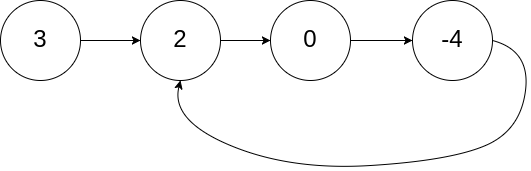
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2:

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3:

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

解题思路

双指针

思路

这类链表题目一般都是使用双指针法解决的，例如 寻找距离尾部第 K 个节点、寻找环入口、寻找公共尾部入口 等。

算法

1. 双指针第一次相遇：设两指针 fast 和 slow 指向链表头部 head，fast 每轮走两步，slow 每轮走一步
   1. 第一种结果：fast 通过走过链表末端，说明链表无环，直接返回 null
      • TIPS：若有环，两指针一定会相遇。因为每走一轮，fast 与 slow 的间距 +1，fast 终会追上 slow
   2. 第二种结果：当 fast == slow 时，两指针在环中第一次相遇，下面分析此时 fast 与 slow 走过的步数关系：
      • 设链表共有 a + b 个节点，其中 链表头部到链表入口 有 a 个节点（不计链表入口节点），链表环 有 b 个节点（这里需要注意，a 和 b 是未知数）；设两指针分别走了 f 和 s 步，则有
        1. fast 走的步数是 slow 步数的两倍，即 f = 2s（解析：fast 每轮走两步）
        2. fast 比 slow 多走了 n 个环的长度，即 f = s + nb（解析：双指针都走过了 a 步，然后在环内绕圈直到重合，重合时 fast 比 slow 多走 环的长度整数倍）
        • 以上两式相减得：s = nb 和 f = 2nb，即 fast 和 slow 指针分别走了 2n，n 个环的周长（注意：n 是未知数，不同链表的情况不同）
2. 目前情况分析：
   • 如果让指针从链表头部一直向前走并统计步数 k，那么所有 走到链表入口节点时的步数 是：k = a + nb（先走 a 步到入口节点，之后每绕 1 圈环（ b 步）都会再次到入口节点）。
   • 而目前，slow 指针走过的步数为 nb 步。因此，我们只要想办法让 slow 再走 a 步停下来，就可以到环的入口。
   • 但是我们不知道 a 的值，该怎么办？依然是使用双指针法。我们构建一个指针，此指针需要有以下性质：此指针和 slow 一起向前走 a 步后，两者在入口节点重合。那么从哪里走到入口节点需要 a 步？答案是链表头部 head。

var detectCycle = function(head) {
  let slow = head,
    fast = head;

  while (true) {
    // 快指针先到达链表尾部，表示链表无环
    if (fast === null || fast.next === null) return null;

    fast = fast.next.next;
    slow = slow.next;

    // 相遇点，也表示链表存在环
    if (fast === slow) break;
  }

  fast = head;

  while (slow != fast) {
    slow = slow.next;
    fast = fast.next;
  }

  return fast;
};

总结：

1. 第一次相遇：slow = nb
2. a + nb = 入口点
3. slow 再走 a = 入口 = head 走到入口 = a
4. 由 3 得出：起始距离入口 = 第一次相遇位置 + a

数学公式推导 + 逻辑结合

参考资料：

• 环形链表 II（双指针法，清晰图解）