设计循环队列

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k 。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull(): 检查循环队列是否已满。

解题思路

数组实现

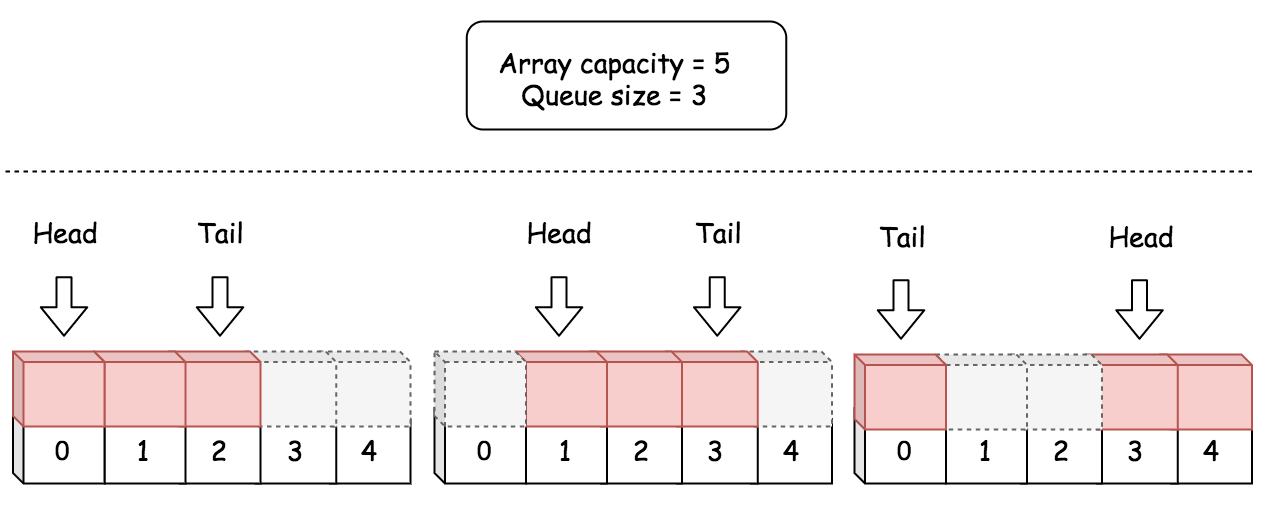
根据问题描述，该问题使用的数据结构应该是首尾相连的 环。

任何数据结构中都不存在环形结构，但是可以使用一维 数组 模拟，通过操作数组的索引构建一个 虚拟 的环。很多复杂数据结构都可以通过数组实现。

对于一个固定大小的数组，任何位置都可以是队首，只要知道队列长度，就可以根据下面公式计算出队尾位置：

const tailIndex = (headIndex + count - 1) % capacity;

其中：

• capacity 是数组长度
• count 是队列长度
• headIndex 是队首 head 索引
• tailIndex 是队尾 tail 索引

实现算法

设计数据结构的关键是如何设计 属性，好的设计属性数量更少。

• 属性数量少说明属性之间冗余更低。
• 属性冗余度越低，操作逻辑越简单，发生错误的可能性更低。
• 属性数量少，使用的空间也少，操作性能更高。

但是，也不建议使用最少的属性数量。 一定的冗余可以降低操作的时间复杂度，达到时间复杂度和空间复杂度的相对平衡。

根据以上原则，列举循环队列的每个属性，并解释其含义。

• queue：一个固定大小的数组，用于保存循环队列的元素。
• headIndex：一个整数，保存队首 head 的索引。
• count：循环队列当前的长度，即 循环队列中的元素数量。使用 headIndex 和 count 可以计算出队尾元素的索引，因此不需要队尾属性。
• capacity：循环队列的容量，即 队列中最多可以容纳的元素数量。该属性不是必需的，因为队列容量可以通过数组属性得到，但是由于该属性经常使用，所以我们选择保留它。这样可以不用在 Python 中每次调用 len(queue) 中获取容量。但是在 Java 中通过 queue.length 获取容量更加高效。为了保持一致性，在两种方案中都保留该属性。

var MyCircularQueue = function(k) {
  this.capacity = k;
  this.queue = new Array(k);
  this.headIndex = 0;
  this.count = 0;
};

MyCircularQueue.prototype.enQueue = function(value) {
  if (this.isFull()) return false;
  this.queue[(this.headIndex + this.count) % this.capacity] = value;
  this.count += 1;
  return true;
};

MyCircularQueue.prototype.deQueue = function() {
  if (this.isEmpty()) return false;
  this.headIndex = (this.headIndex + 1) % this.capacity;
  this.count -= 1;
  return true;
};

MyCircularQueue.prototype.Front = function() {
  if (this.isEmpty()) {
    return -1;
  }
  return this.queue[this.headIndex];
};

MyCircularQueue.prototype.Rear = function() {
  if (this.isEmpty()) {
    return -1;
  }
  return this.queue[(this.headIndex + this.count - 1) % this.capacity];
};

MyCircularQueue.prototype.isEmpty = function() {
  return this.count == 0;
};

MyCircularQueue.prototype.isFull = function() {
  return this.count == this.capacity;
};

复杂度分析

• 时间复杂度：O(1)。该数据结构中，所有方法都具有恒定的时间复杂度。
• 空间复杂度：O(N)。其中 N 是队列的预分配容量。循环队列的整个生命周期中，都持有该预分配的空间。