Data Structure and Algorithms Guidebook

数据结构与算法完全知识体系

二叉树

二叉树（Binary tree）是每个节点最多只有两个分支（即不存在分支度大于 2 的节点）的树结构。通常分支被称作 左子树 或 右子树。二叉树的分支具有左右次序，不能随意颠倒。

树和二叉树的三个主要差别：

  • 树的节点个数至少为 1，而二叉树的节点个数可以为 0
  • 树中的最大度数（节点数量）没有限制，而二叉树的节点的最大度数为 2
  • 树的节点没有左右之分，而二叉树的节点有左右之分

性质

  • 若二叉树的层次从 0 开始，则在二叉树的第 i 层至多有 2^i 个结点（i >= 0）
    • i = 1 时，只有一个根节点 2^(i - 1) = 2^ 0 = 1
  • 高度为 k 的二叉树最多有 2^(k + 1) - 1 个结点（k>=-1）（空树的高度为 -1）
    • i = 2 时，2^k - 1 = 2^2 - 1 = 3 个节点
  • 对任何一棵二叉树，如果其叶子结点（度为 0）数为 m，度为 2 的结点数为 n, 则 m = n + 1

特殊类型

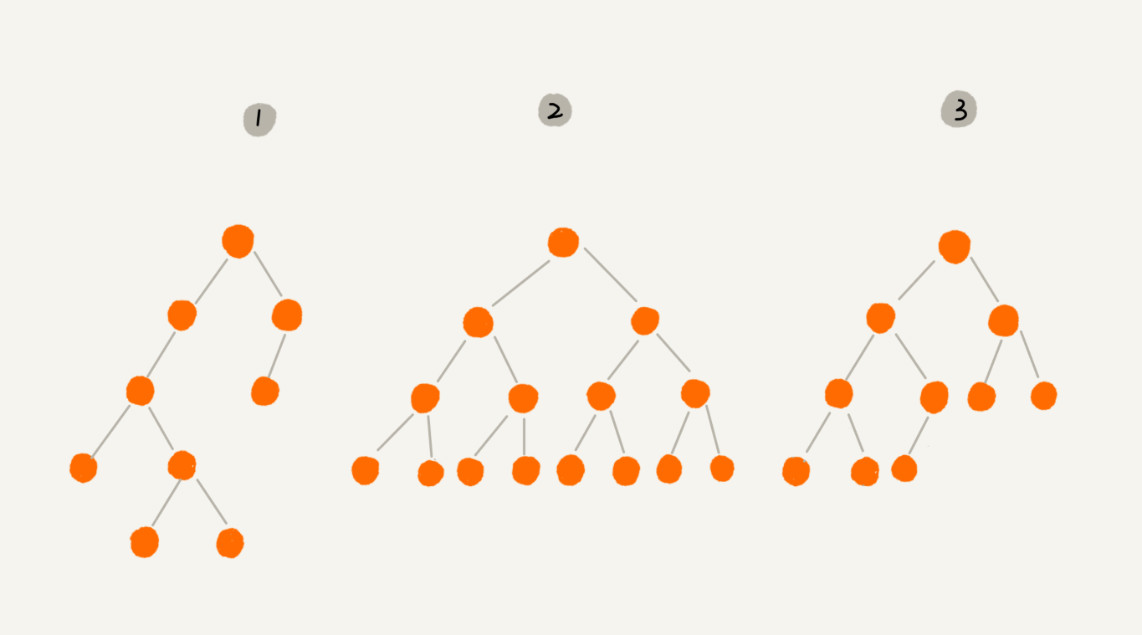
满二叉树和完全二叉树

满二叉树

上图编号 2 的二叉树中，叶子节点全部都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫做 满二叉树（Full Binary Tree）。

满二叉树的性质：

  1. 一棵树深度为 h，最大层数为 k，深度与最大层数相同 k = h
  2. 叶子数为 2^h
  3. 第 k 层的节点数是 2^(k-1)
  4. 总节点数是 2^(k - 1)，且总节点数一定是奇数

完全二叉树

上图编号 3 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都达到最大，这种二叉树叫做 完全二叉树（Complete Binary Tree）。

完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra 算法、Prim 算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

以上两种特殊类型的二叉树都能通过公式计算总节点和树高。

满二叉树完全二叉树
总节点 k2^(h - 1) <= k <= 2^h - 1k = 2^h - 1
树高 hh = log2 k + 1h = log2(k + 1)

二叉树搜索

  • 深度优先搜索
    • 中序遍历：即 左-根-右 遍历，对于给定的二叉树根，寻找其左子树；对于其左子树的根，再去寻找其左子树；递归遍历，直到寻找最左边的节点 i，其必然为叶子，然后遍历 i 的父节点，再遍历 i 的兄弟节点。随着递归的逐渐出栈，最终完成遍历：
    • 前序遍历：即 根-左-右 遍历
    • 后序遍历：即 左-右-根 遍历
  • 广度优先搜索
    • 层次遍历

实际上，二叉树的前、中、后序遍历就是一个递归的过程。

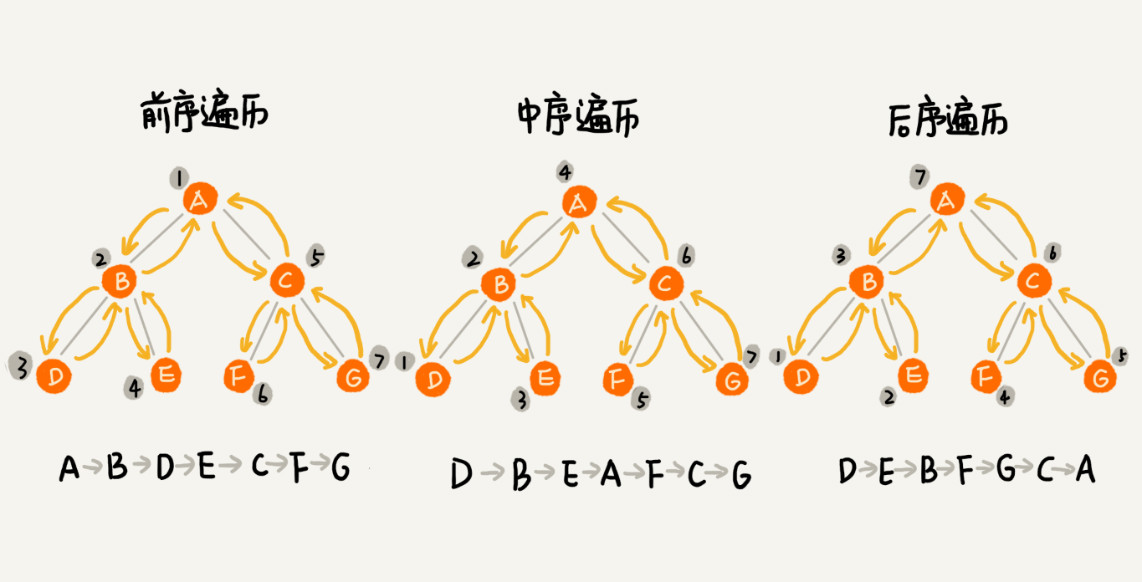
二叉树的遍历

前序遍历

前序遍历首先访问根节点，然后遍历左子树，最后遍历右子树。

递归实现

先访问根节点，接着递归左子树、右子树。

var preorderTraversal = function (root) {
  if (root == null) return [];
  const ans = [];
  var dfs = function (node) {
    if (node == null) return;
    ans.push(node.val);
    dfs(node.left);
    dfs(node.right);
  };
  dfs(root, ans);
  return ans;
};

栈实现

非递归的思路：

  1. 定义一个栈，先将根节点压入栈
  2. 若栈不为空，每次从栈中弹出一个节点
  3. 处理该节点
  4. 先把节点右孩子压入栈，接着把节点左孩子压入栈（如果有孩子节点）
  5. 重复 2-4
  6. 返回结果
// 使用栈完成前序遍历
var preorderTraversal = function (root) {
  if (root === null) return [];
  // stack 用于进行递归的栈
  // ans 用于存放遍历的结果，不算在空间复杂度中
  let stack = [],
    ans = [];
  // 开始利用栈进行遍历
  while (root || stack.length) {
    // 模拟递归的压栈过程
    while (root) {
      ans.push(root.val);
      stack.push(root);
      root = root.left;
    }
    // 当无法压栈的时候，将 root.right 进行压栈
    root = stack.pop();
    root = root.right;
  }
  return ans;
};

Morris 实现

Morris 遍历无需使用栈，空间复杂度为 。核心思想是：

遍历二叉树节点，

  1. 若当前节点 root 的左子树为空，将当前节点值添加至结果列表 ans 中，并将当前节点更新为 root.right
  2. 若当前节点 root 的左子树不为空，找到左子树的最右节点 pre（也即是 root 节点在中序遍历下的前驱节点）：
    • 若前驱节点 pre 的右子树为空，将当前节点值添加至结果列表 ans 中，然后将前驱节点的右子树指向当前节点 root，并将当前节点更新为 root.left。
    • 若前驱节点 pre 的右子树不为空，将前驱节点右子树指向空（即解除 pre 与 root 的指向关系），并将当前节点更新为 root.right。
  3. 循环以上步骤，直至二叉树节点为空，遍历结束。
var preorderTraversal = function (root) {};

中序遍历

左子树作为一个整体放到左边，然后把根结点放到中间，最后把右子树作为一个整体放右边。接着再把左子树展开。最后把右子树展开，此时我们得到了最终中序遍历的结果。

中序遍历的遍历顺序：

  1. 左子树
  2. 根节点
  3. 右子树

是先遍历左子树，然后访问根节点，然后遍历右子树。

通常来说，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。

递归实现

实现思路：先递归左子树，再访问根节点，接着递归右子树。

var inorderTraversal = function (root) {
  if (!root) return [];
  const ans = [];
  function dfs(node) {
    if (node) {
      dfs(node.left);
      ans.push(node.val);
      dfs(node.right);
    }
  }
  dfs(root);
  return ans;
};

栈实现

栈实现非递归遍历

非递归的思路如下：

  1. 定义一个栈
  2. 将树的左节点依次入栈
  3. 左节点为空时，弹出栈顶元素并处理
  4. 重复 2-3 的操作
var inorderTraversal = function (root) {
  let stack = [],
    ans = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    ans.push(root.val);
    root = root.right;
  }
  return ans;
};

Morris 实现

var inorderTraversal = function (root) {};

后序遍历

后序遍历是先遍历左子树，然后遍历右子树，最后访问树的根节点。

值得注意的是，当你删除树中的节点时，删除过程将按照后序遍历的顺序进行。 也就是说，当你删除一个节点时，你将首先删除它的左节点和它的右边的节点，然后再删除节点本身。

另外，后序在数学表达中被广泛使用。 编写程序来解析后缀表示法更为容易。 这里是一个例子：

您可以使用中序遍历轻松找出原始表达式。 但是程序处理这个表达式时并不容易，因为你必须检查操作的优先级。

如果你想对这棵树进行后序遍历，使用栈来处理表达式会变得更加容易。 每遇到一个操作符，就可以从栈中弹出栈顶的两个元素，计算并将结果返回到栈中。

递归实现

var postorderTraversal = function (root) {
  if (!root) return [];
  const ans = [];
  function dfs(node) {
    if (!node) return;
    dfs(node.left);
    dfs(node.right);
    ans.push(node.val);
  }
  dfs(root);
  return ans;
};

栈实现

var postorderTraversal = function (root) {
  if (!root) return [];


  let stack = [root],
    ans = [];
  while (stack.length) {
    const node = stack.pop();
    // 根左右 -> 右左根
    ans.unshift(node.val);


    // 先进栈左子树后右子树
    // 出栈顺序变更为先右后左
    // 右先头插法插入 ans
    // 左再头插法插入 ans
    // 实现右左根 -> 左右根
    if (node.left) {
      stack.push(node.left);
    }
    if (node.right) {
      stack.push(node.right);
    }
  }
  return ans;
};

层序遍历

var levelOrder = function (root) {
  if (!root) return [];


  let ans = [],
    queue = [root];


  while (queue.length) {
    let len = queue.length;


    while (len) {
      const node = queue.shift();
      ans.push(node.val);
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);


      len--;
    }
  }
  return ans;
};

参考资料

Edit this doc on GitHub2/21/2022 13:38:33