AVL 树

AVL 树是带有平衡条件的二叉查找树，和红黑树相比，它是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差不超过 1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的。

性质

AVL 树是二叉平衡查找树，所以继承了二叉查找树的性质，同时具有平衡属性：

任意节点左子树上的节点值比该节点小，右子树上的节点值比该节点大
左右子树高度之差的绝对值不能超过 1（当该值为 2 时表示平衡树失去了平衡）

节点的 平衡因子 是它的左子树的高度减去它的右子树的高度。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

距离插入节点最近的，且平衡因子的绝对值不大于 1 的节点为根的子树，我们称为最小不平衡子树

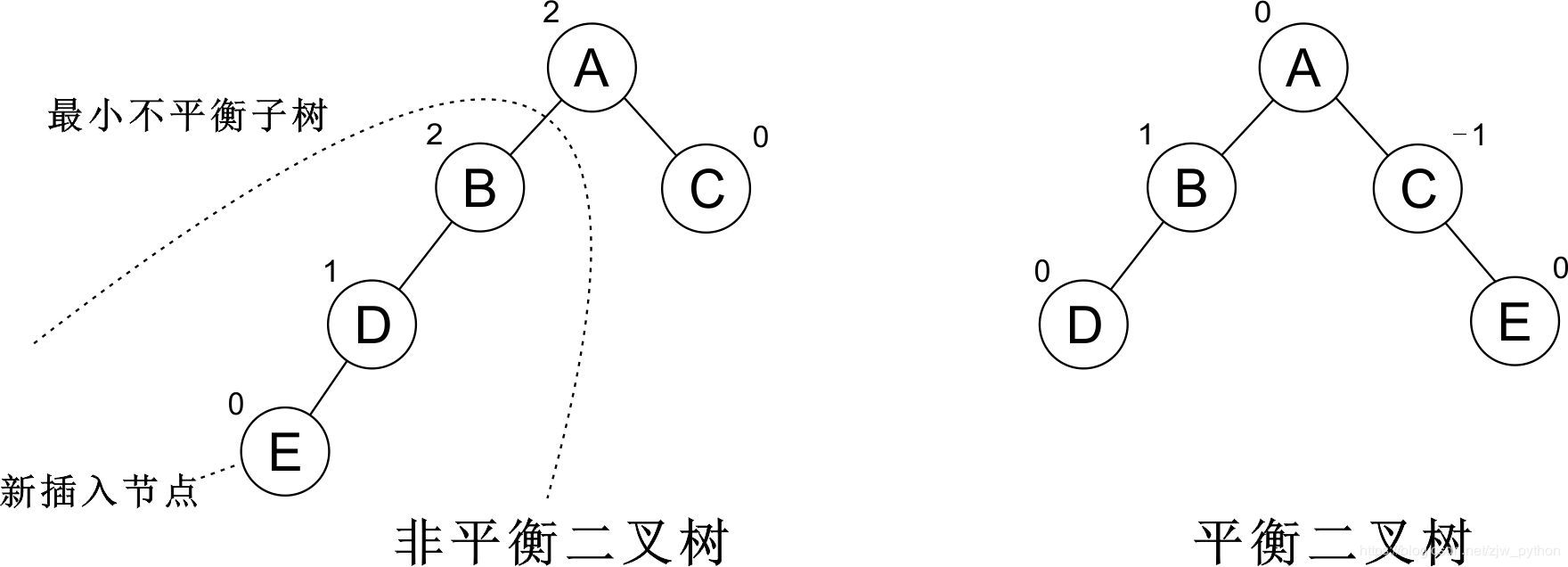
平衡调整

平衡二叉树的构建过程基于二叉查找树的构建过程，在插入节点的过程中，一旦出现不平衡现象（即某节点的平衡因子大于 1 或小于 -1），就需要找出 最不平衡子树，进行平衡调整，也叫 旋转 操作，调整最小不平衡子树中各节点的链接关系，使之称为新的平衡子树。旋转的过程就好比一条扁担出现一头重一头轻的现象，若能将扁担的支撑点改变，扁担两头就平衡了。

有四种情况可能导致二叉查找树不平衡，分别为：

LL：插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由 1 变为 2
RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由 -1 变为 -2
LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由 1 变为 2
RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由 -1 变为 -2

这里指的根节点指的是 最小不平衡子树 的根节点，而非整棵树的根节点。

针对四种种情况可能导致的不平衡，可以通过旋转使之变平衡。有两种基本的旋转：

左旋转：将根节点旋转到（根节点的）右子节点的左子节点位置
右旋转：将根节点旋转到（根节点的）左子节点的右子节点位置

以上四种情况分别对应不同的不平衡情况，其中 LL 和 RR 只需要进行一次旋转即可重获平衡，而 LR 和 RL 则需要两次旋转。每种类型可以细分为三种情况，总共 12 种情况。

平衡调整的秘笈：

属性克制（分类）：找插入新节点后 失去平衡的最小子树
落井下石（右旋、左旋）
谋权、篡位、变节（RL、LR）

LL 左左

第 1、2 种情况，左左 表示最小不平衡子树的根节点左子节点的左子节点是新插入节点的父节点

第 3 种情况，左左表示最小不平衡子树的根节点左子节点的左子节点是新插入的节点

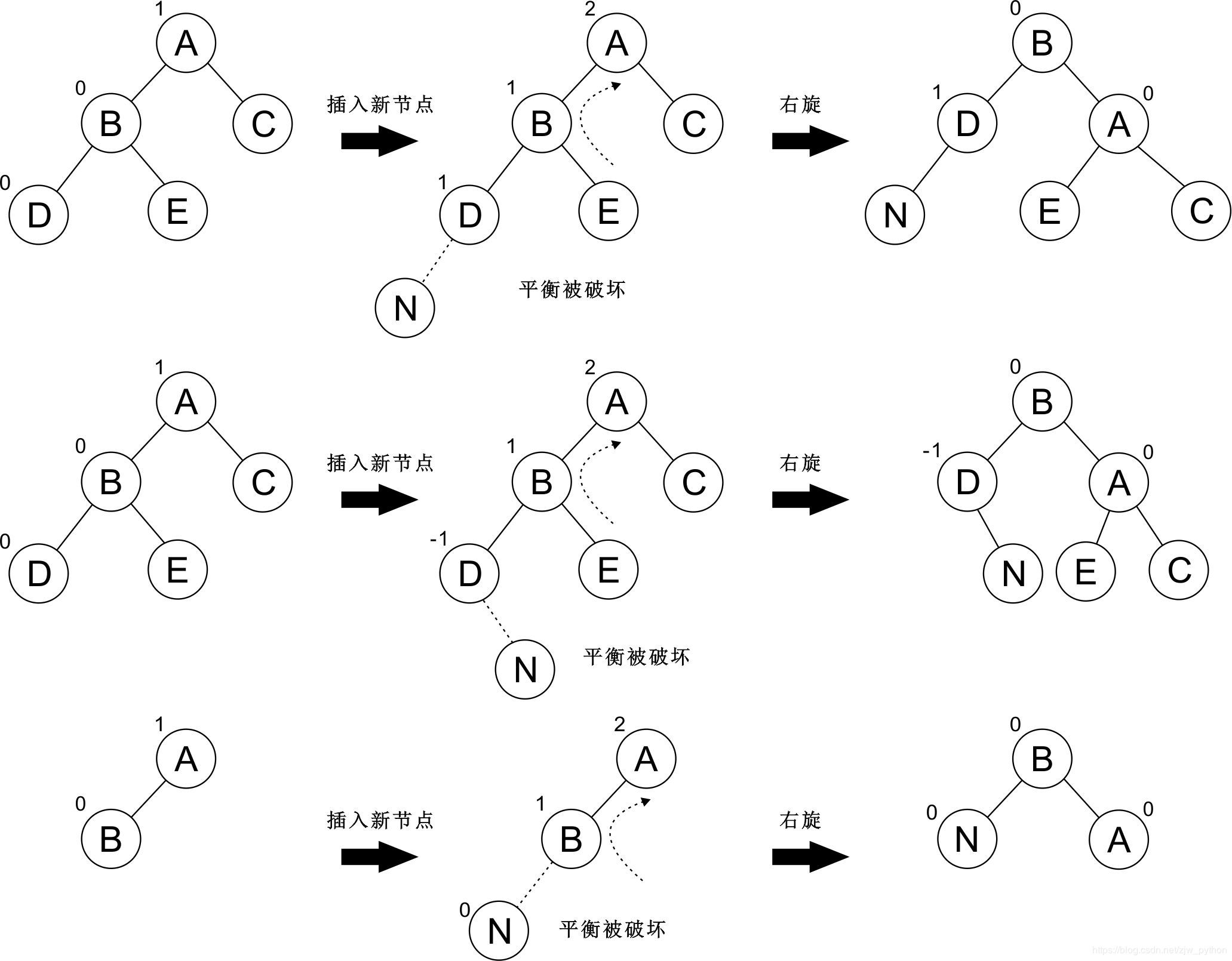
当出现上图情况一、二的时候：

最小不平衡子树的根节点（图例中的节点 A）就带着它的子树，占据了该根节点的 左子节点的右子节点
然后把原来的节点（节点 E）嫁接在该节点（节点 A）上。

当出现上图情况三的时候，只需要将最小不平衡子树的根节点变为它的子节点的右子节点即可。

RR 右右

和 LL 类似：

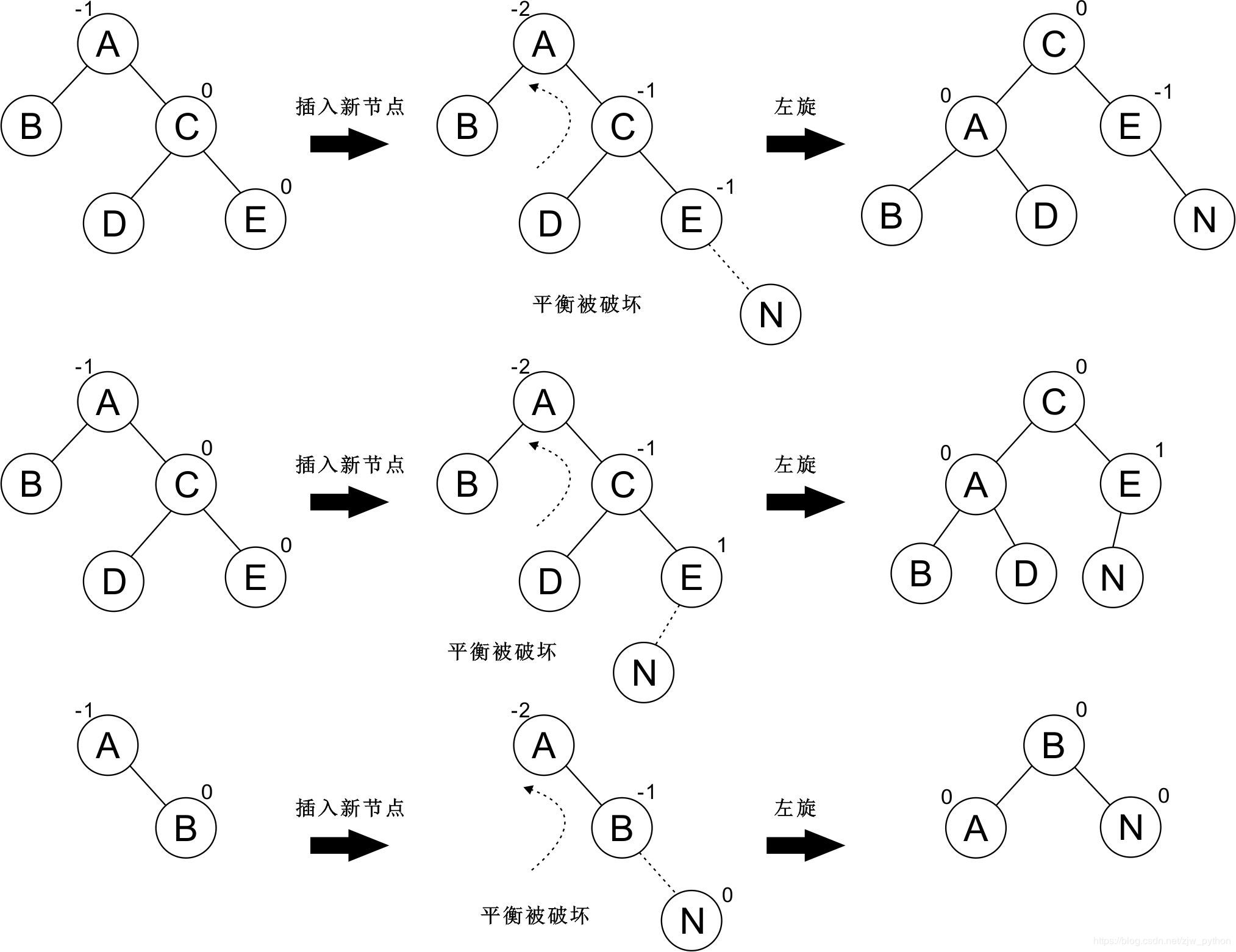
当出现上图情况一、二的时候：

最小不平衡子树的根节点（图例中的节点 A）就带着它的子树，占据了该根节点的 右子节点的左子节点
然后把原来的节点（节点 D）嫁接在该节点（节点 A）上。

当出现上图情况三的时候，只需要将最小不平衡子树的根节点变为它的子节点的左子节点即可。

LR 左右

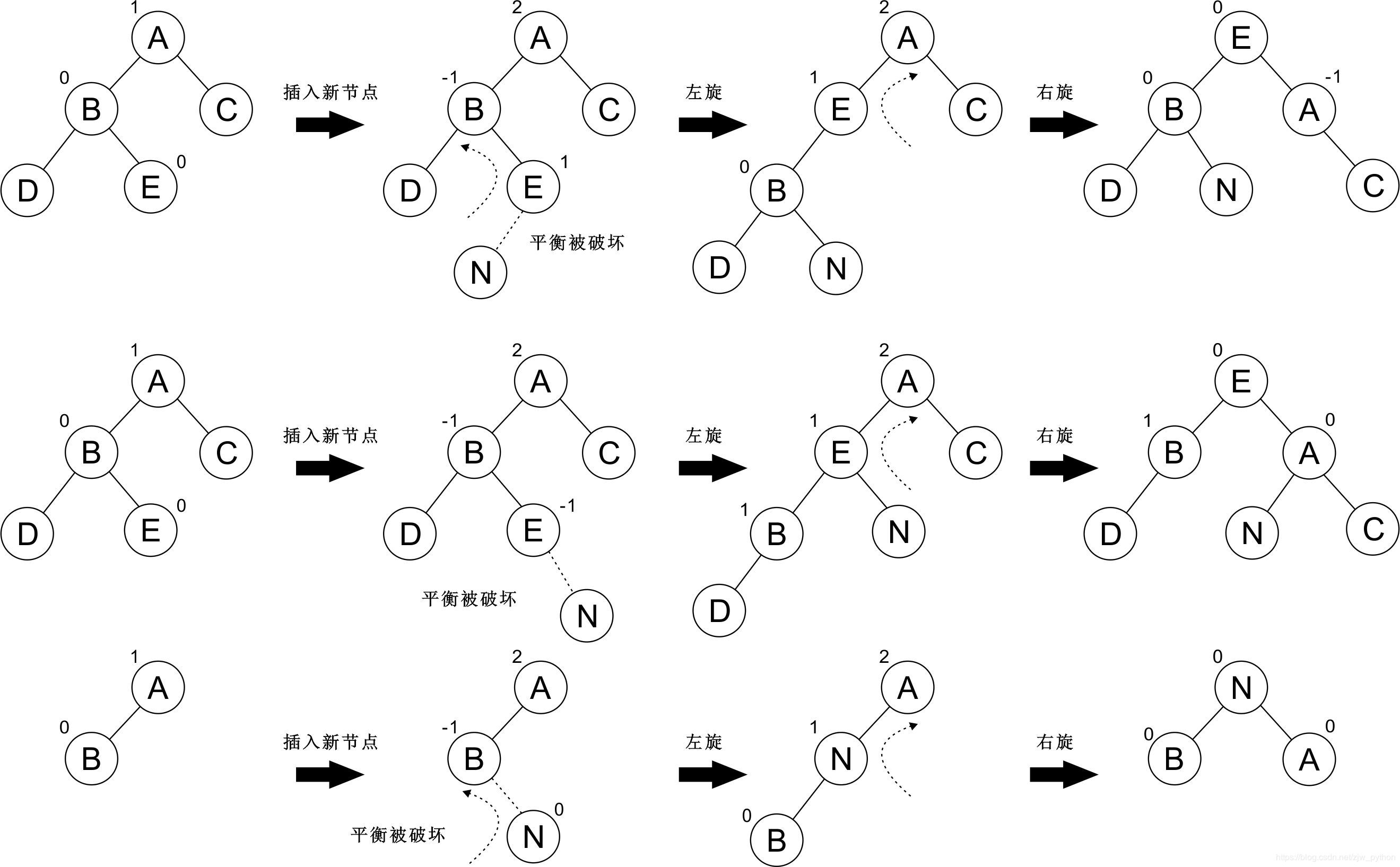
RL 右左

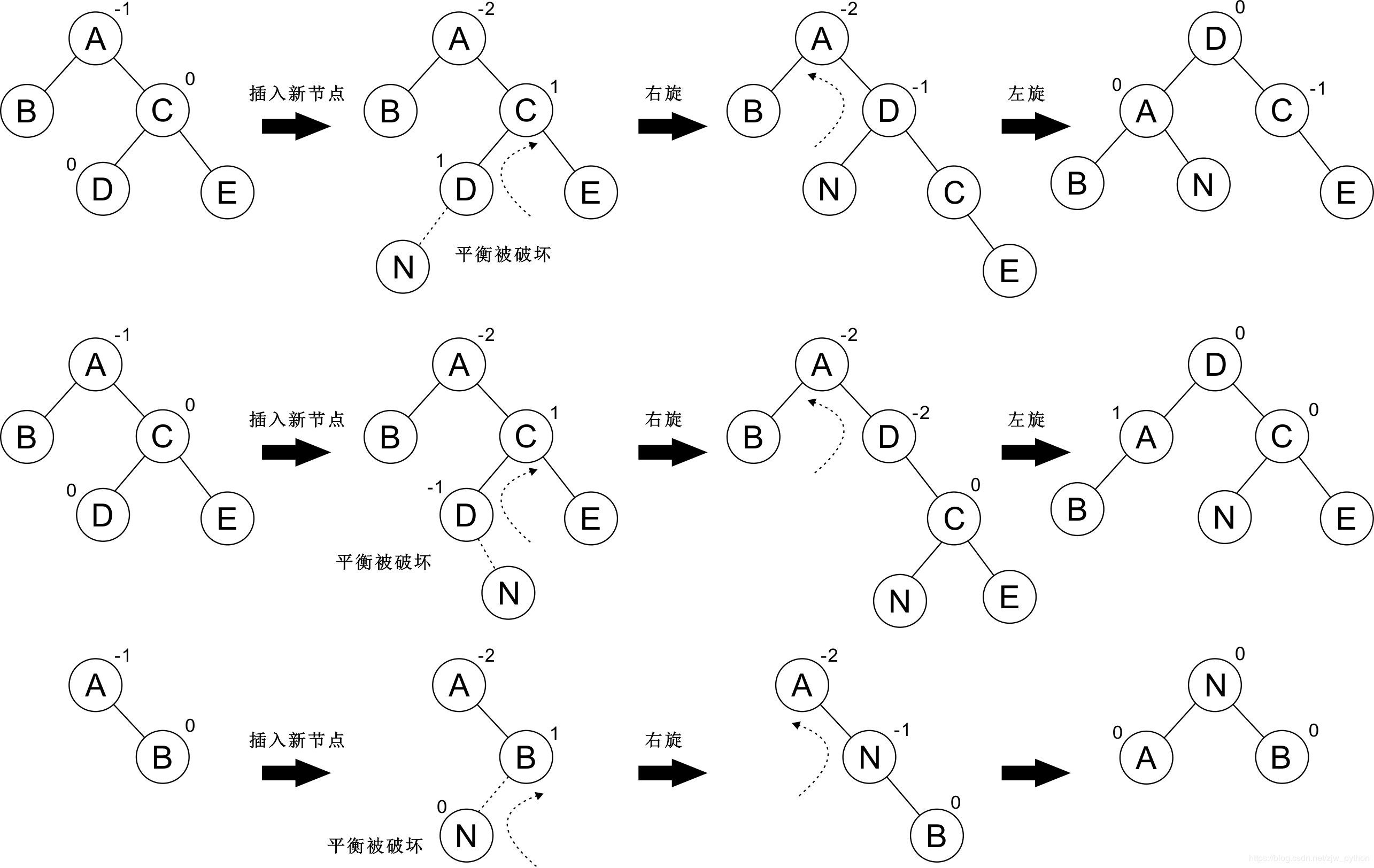
平衡调整总结

当 LL 或 RR 时：

只需要旋转一次，旋转方向与类型名称相反，也就是 LL 右旋、RR 左旋
步骤一：最小不平衡子树的根节点替换掉位于它整下方的，它的子节点的子节点（落井）
步骤二：然后将被替换掉的节点接到它的非空子节点上（下石）
调整后的子树的根节点一定是最小不平衡子树高度更高一边的左子节点

当 LR 或 RL 时：

需要旋转两次，旋转方向和顺序与类型名称相同，也就是 LR 先左旋后右旋，RL 先右旋后左旋
步骤一：新增节点的父节点，先抛弃它的子节点，安插在根节点和根节点的左子节点之间（谋权）
步骤二：然后将根节点变为它的空侧的子节点（篡位），然后将原新增的节点（就是被抛弃的子节点），变换原来的方向 嫁接在新根节点的子节点上（变节）
调整后的子树的根节点一定是新增节点的父节点，所以称之为谋权篡位

特点

AVL 树本质上还是一棵二叉搜索树，它的特点是：

AVL 树是一棵二叉搜索树
AVL 树的左右子节点也是 AVL 树
AVL 树拥有二叉搜索树的所有基本特点
每个节点的左右子节点的高度之差的绝对值最多为 1，即平衡因子为范围为 [-1,1]

操作

AVL 树的基本操作是旋转，有四种旋转方式，分别为：左旋转，右旋转，左右旋转（先左后右），右左旋转（先右后左），实际上，这四种旋转操作两两对称，因而也可以说成两类旋转操作。

定义 AVL 树：

/**
 * 用于创建树节点实例
 * @param key 用于检索节点的标识符
 * @param value 存储在节点内的数据，可以是任意类型
 */
const Node = function(key, value) {
  this.key = key;
  this.value = value;
  this.left = null;
  this.right = null;
  this.height = null;
};

/**
 * 计算左子树高度，如果为空则返回 -1
 */
Node.prototype.leftHeight = function() {
  return this.left ? this.left.height : -1;
};

/**
 * 计算右子树高度，如果为空则返回 -1
 */
Node.prototype.rightHeight = function() {
  return this.right ? this.right.height : -1;
};

/**
 * 对比两棵子树，返回高度较高的子树的高度
 */
Node.prototype.getMaxHeight = function(a, b) {
  return Math.max(a, b) + 1;
};

function AVLTree() {
  this.root = null;
  this.size = 0;
}

AVLTree.prototype.size = function() {
  return this.size;
};

AVLTree.prototype.isEmpty = function() {
  return this.size === 0;
};

属性定义

AVLTree.prototype.compare = function(a, b) {
  if (a > b) {
    return 1;
  } else if (a < b) {
    return -1;
  } else {
    return 0;
  }
};

定义每棵树的平衡状态：

const BalancedState = {
  UNBALANCED_RIGHT: 1,
  SLIGHTLY_UNBALANCED_RIGHT: 2,
  BLANCED: 3,
  SLIGHTLY_UNBALANCED_LEFT: 4,
  UNBALANCED_LEFT: 5
}

function getBalanceState(node) {
  // 计算平衡因子
  const balancedFactor = node.leftHeight() - node.rightHeight();

  swith(balancedFactor) {
    // 右子树比左子树高，右子树严重失衡
    case -2: return BalancedState.UNBALANCED_RIGHT;
    // 右子树比左子树高，右子树轻度失衡
    case -1: return BalancedState.SLIGHTLY_UNBALANCED_RIGHT;
    // 左子树比右子树高，左子树轻度失衡
    case 1: return BalancedState.SLIGHTLY_UNBALANCED_LEFT;
    // 左子树比右子树高，左子树严重失衡
    case 2: return BalancedState.UNBALANCED_LEFT;
    //
    default: return BalancedState.BALANCED;
  }
}

左旋转

/**
 * 节点左旋，该节点旋转前的右节点肯定是旋转后以当前节点为根节点的树的根节点
 *       b                           a
 *      / \                         / \
 *     a   e -> b.rotateRight() -> c   b
 *    / \                             / \
 *   c   d                           d   e
 */
Node.prototype.rotateLeft = function() {
  let newRoot = this.right;
  this.right = newRoot.left;
  newRoot.left = this;

  this.height = this.getMaxHeight(this.rightHeight(), this.leftHeight());
  // 右子节点保持不变，左子节点变为原来根节点
  newRoot.height = this.getMaxHeight(newRoot.rightHeight(), this.height);

  return newRoot;
};

右旋转

/**
 * 右旋
 *       b                           a
 *      / \                         / \
 *     a   e -> b.rotateRight() -> c   b
 *    / \                             / \
 *   c   d                           d   e
 */
Node.prototype.rotateRight = function() {
  let newRoot = this.left;
  this.left = newRoot.right;
  newRoot.right = this;

  this.height = this.getMaxHeight(this.leftHeight(), this.rightHeight());
  // 左子节点保持不变，右子节点变为原来根节点
  newRoot.height = this.getMaxHeight(newRoot.leftHeight(), this.height);

  return newRoot;
};

插入操作

先判断边界问题，当根节点为空时，创建新节点
根据目标节点索引大小，递归左右子树，若索引相同则不插入新元素
更新节点高度后，根据当前节点子树的平衡状态进行处理

/**
 * 插入指定键值的新节点
 */
AVLTree.prototype.insert = function(key, value) {
  this.root = this.recrusiveInsert(key, value, this.root);
  this.size++;
};

/**
 * 插入指定键值的新节点
 */
AVLTree.prototype.recrusiveInsert = function(key, value, root) {
  // 空树，创建新节点
  if (root === null) {
    return new Node(key, value);
  }

  // 根据目标节点索引的大小，递归左右子树
  if (this.compare(key, root.key) < 0) {
    // 目标节点索引比当前节点索引小，递归左子树
    root.left = this.recrusiveInsert(key, value, root.left);
  } else if (this.compare(key, root.key) > 0) {
    // 目标节点索引比当前节点索引大，递归右子树
    root.right = this.recrusiveInsert(key, value, root.right);
  } else {
    // 重复节点，插入失败，缩减 AVL 树尺寸
    this.siez--;
    return root;
  }

  // 更新高度
  root.height = Math.max(root.leftHeight(), root.rightHeight()) + 1;
  // 获取当前节点平衡状态
  const balancedState = getBalanceState(root);

  // 左子树失衡，LL 型或 LR 型
  if (balancedState === BalancedState.UNBALANCED_LEFT) {
    if (this.compare(key, root.left.key) < 0) {
      // 插入节点的索引比当前节点的左子节点的索引小（如下图所示，A 为当前子树根节点，B 为当前子树根节点的左子节点，N 为新增节点）
      //         A
      //        / \
      //       B   C
      //      / \
      //     D   E
      //    / \
      //  N1   N2
      // LL 型，根节点右旋
      root = root.rotateRight();
    } else {
      // 插入节点的索引比当前节点的左子节点的索引大（如下图所示，A 为当前子树根节点，B 为当前子树根节点的左子节点，N 为新增节点）
      //         A
      //        / \
      //       B   C
      //      / \
      //     D   E
      //        / \
      //      N1   N2
      // LR 型，以根节点的左节点为轴心，先左旋，后右旋
      root.left = root.left.rotateLeft();
      return root.rotateRight();
    }
  }

  // 右子树失衡，RR 型或 RL 型
  if (balancedState === BalancedState.UNBALANCED_RIGHT) {
    if (this.compare(key, root.right.key) < 0) {
      // 插入节点的索引比当前节点的右子节点的索引小（如下图所示，A 为当前子树根节点，C 为当前子树根节点的右子节点，N 为新增节点）
      //         A
      //        / \
      //       B   C
      //          / \
      //         D   E
      //            / \
      //          N1   N2
      // RR 型，根节点左旋
      root = root.rotateLeft();
    } else {
      // 插入节点的索引比当前节点的左子节点的索引大（如下图所示，A 为当前子树根节点，C 为当前子树根节点的右子节点，N 为新增节点）
      //         A
      //        / \
      //       B   C
      //          / \
      //         D   E
      //        / \
      //      N1   N2
      // RL 型，以根节点的右节点为轴心，先右旋，后左旋
      root.right = root.right.rotateRight();
      return root.rotateLeft();
    }
  }

  return root;
};

删除操作

先判断边界问题，当根节点为空时，创建新节点
根据目标节点索引大小，递归左右子树，若索引相同则不插入新元素
更新节点高度后，根据当前节点子树的平衡状态进行处理

AVLTree.prototype.delete = function(key) {
  this.root = this.recrusiveDelete(key, this.root);
  this.size--;
};

AVLTree.prototype.recrusiveDelete = function(key, root) {
  // 空树
  if (root === null) {
    this.size++;
    return root;
  }

  // 根据目标节点索引的大小，递归左右子树
  if (this.compare(key, root.key) < 0) {
    // 目标节点索引比当前节点索引小，递归左子树
    root.left = this.recrusiveDelete(key, root.left);
  } else if (this.compare(key, root.ket) > 0) {
    // 目标节点索引比当前节点索引大，递归右子树
    root.right = this.recrusiveDelete(key, root.right);
  } else {
    // 当前节点是将被删除的节点，根据当前节点的左右节点是否存在分情况处理
    if (!root.left && !root.right) {
      // 将被删除的节点既无左节点，又无右节点
      root = null;
    } else if (!root.left && root.right) {
      // 将被删除的节点无左节点，有右节点
      root = root.right;
    } else if (root.left && !root.right) {
      // 将被删除的节点有左节点，无右节点
      root = root.left;
    } else {
      // 将被删除的节点既有左节点，又有右节点
      // 找到右子树中最小的节点（中续后继节点），替换当前节点
      // 为什么是找右子树中最小的节点呢，因为根据二分查找树的特点
      // 当前节点右子树中值最小的节点既大于当前节点左子树中的所有节点，也小于当前节点右子树中所有节点（当前除了选中的这个最小值节点）
      let inOrderSuccessor = minValueNode(root.right);
      root.key = inOrderSuccessor.key;
      root.value = inOrderSuccessor.value;
      // 删除同索引的值，因为已经替换了当前的节点
      root.right = this.recrusiveDelete(inOrderSuccessor.key, root.right);
    }
  }

  if (root === null) return root;

  // 更新高度和进行平衡调整
  root.height = Math.max(root.leftHeight(), root.rightHeight()) + 1;
  const balancedState = getBalanceState(root);

  // 左子树失衡，LL 型或 LR 型
  if (balancedState === BalancedState.UNBALANCED_LEFT) {
    // LL 型
    if (
      getBalanceState(root.left) === BalancedState.BALANCED ||
      getBalanceState(root.left) === BalancedState.SLIGHTLY_UNBALANCED_LEFT
    ) {
      return root.rotateRight();
    }

    // LR 型
    if (getBalanceState(root.left) === BalancedState.SLIGHTLY_UNBALANCED_RIGHT) {
      root.left = root.left.rotateLeft();
      return root.rotateRight();
    }
  }

  // 右子树失衡，RR 型或 RL 型
  if (balancedState === BalancedState.UNBALANCED_RIGHT) {
    // RR 型
    if (
      getBalanceState(root.right) === BalancedState.BALANCED ||
      getBalanceState(root.right) === BalancedState.SLIGHTLY_UNBALANCED_RIGHT
    ) {
      return root.rotateLeft();
    }

    // RL 型
    if (getBalanceState(root.right) === BalancedState.SLIGHTLY_UNBALANCED_LEFT) {
      root.right = root.right.rotateRight();
      return root.rotateLeft();
    }
  }

  return root;
};

查找操作

AVLTree.prototype.get = function(key) {
  if (this.root === null) {
    return null;
  }

  return this.getNode(key, this.root).value;
};

AVLTree.prototype.getNode = function(key, root) {
  const result = this.compare(key, root.key);

  if (result === 0) {
    return root;
  }

  if (result < 0) {
    if (!root.left) {
      return null;
    }

    return this.getNode(key, root.left);
  }

  if (!root.right) {
    return null;
  }

  return this.getNode(key, root.right);
};

/**
 * 判断指定索引对应节点是否存在
 */
AVLTree.prototype.contains = function(key) {
  if (this.root === null) {
    return false;
  }

  return !!this.getNode(key, this.root);
};

AVLTree.prototype.findMinimum = function() {
  return minValueNode(this.root).key;
};

function minValueNode(root) {
  let current = root;

  while (current.left) {
    current = current.left;
  }

  return current;
}

AVLTree.prototype.findMaximum = function() {
  return maxValueNode(this.root).key;
};

function maxValueNode(root) {
  let current = root;

  while (current.right) {
    current = current.right;
  }

  return current;
}

使用场景

AVL 树适合用于插入删除次数比较少，但查找多的情况。

也在 Windows 进程地址空间管理中得到了使用

旋转的目的是为了降低树的高度，使其平衡

参考资料：

Data Structure and Algorithms Guidebook