二叉搜索树

二叉搜索树（Binary Search Tree），也称为二叉查找树、有序二叉树（Ordered Binary Tree）或排序二叉树（Sorted Binary Tree），是指一棵空树或者具有下列性质的二叉树：

若任意节点的 左子树 不为空，则左子树上所有节点的值 均小于 它的根节点的值
若任意节点的 右子树 不为空，则右子树上所有节点的值 均大于或等于 它的根节点的值
任意节点的左、右子树也分别为二叉搜索树
没有键值相等的节点

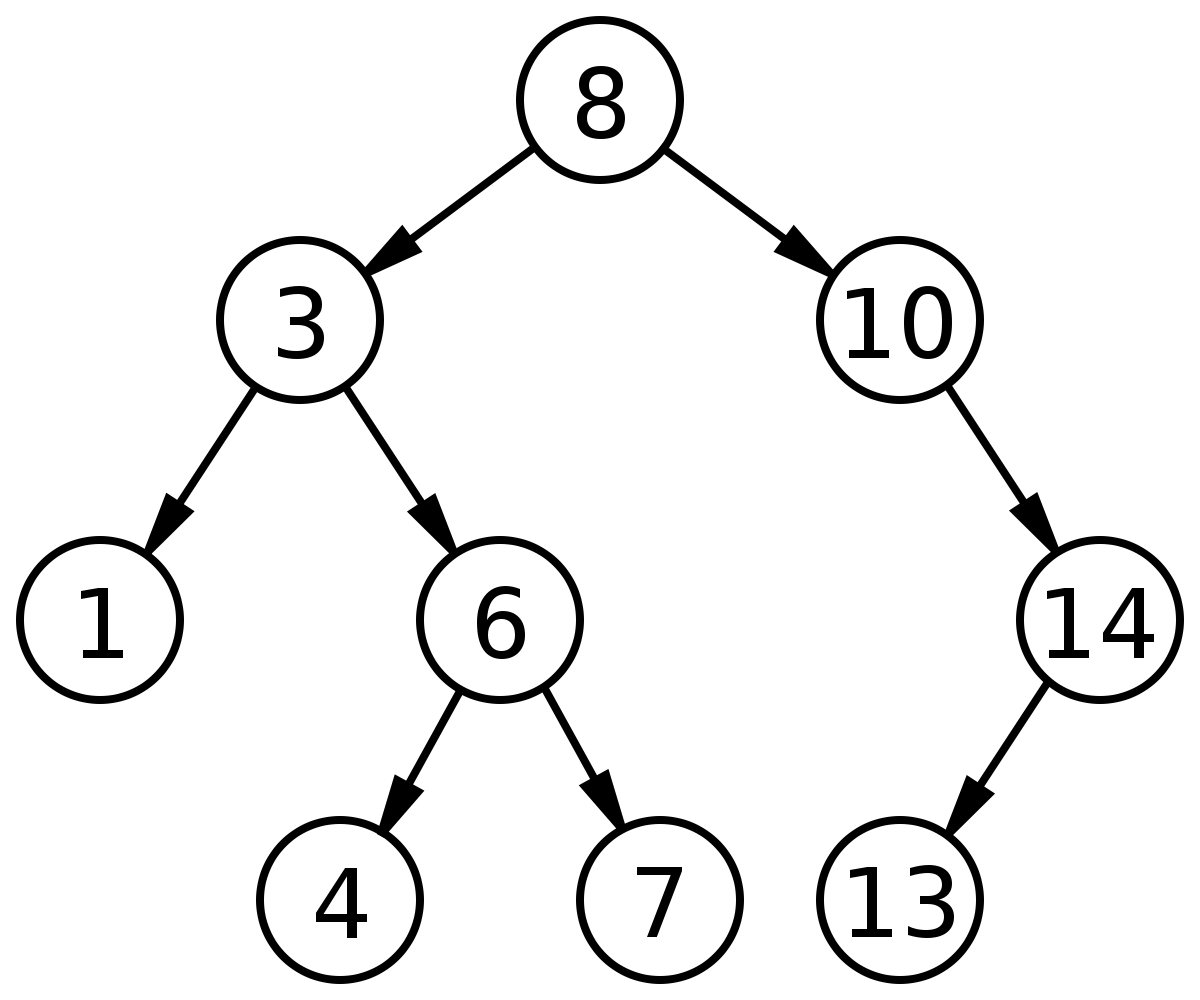
二叉搜索树不一定是完全二叉树，所以用数组并不方便，因此通常设立 TreeNode 节点表示 key-value，节点间联系通常使用指针和引用。

优势

二叉搜索树的优点是，即便在最坏的情况下，也允许你在 O(h) 的时间复杂度内执行所有的搜索、插入、删除操作。

通常来说，如果你想有序地存储数据或者需要同时执行搜索、插入、删除等多步操作，二叉搜索树这个数据结构是一个很好的选择。

	查找元素	插入元素	删除元素
普通数组	`O(n)`	`O(n)`	`O(n)`
顺序数组	`O(log n)`	`O(n)`	`O(n)`
二分搜索树	`O(log n)`	`O(log n)`	`O(log n)`

高效：不仅可查找数据；还可以高效地插入、删除数据（动态维护数据）

可以方便地解决很多数据之间的关系问题：min、max、floor、ceil、rank、select

实现

二叉搜索树主要支持三个操作：搜索、插入和删除。

根据上面的知识，我们了解到二叉树实际上是由多个节点组成，因此我们首先要定义一个 TreeNode 类，用于存放树的节点，其构造与链表类似。

TreeNode 类的定义如下：

function TreeNode(value, left, right) {
  this.value = value;
  this.left = left;
  this.right = right;
}

用户对象既保存了数据，也保存了它的左节点和右节点的引用。

现在我们可以创建一个类，用来表示二叉搜索树（BST），我们初始化类只包含一个成员，一个表示二叉搜索树节点的 TreeNode 对象，初始化为 null，表示创建一个空节点。

function BST() {
  // 根节点
  this.root = null;
}

插入操作

二叉搜索树中的基本操作是插入一个新节点。有许多不同的方法去插入新节点，这章节中，我们只讨论一种使整体操作变化最小的经典方法。它的主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。

与搜索操作类似，对于每个节点，我们将：

根据节点值与目标节点值的关系，搜索左子树或右子树；
重复步骤 1 直到到达外部节点；
根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

这样，我们就可以添加一个新的节点并依旧维持二叉搜索树的性质。

BST.prototype.insert = function (value) {
  // 首先要添加新的节点，首先需要创建 TreeNode 对象，将数据传入该对象
  const newNode = new TreeNode(value, null, null);

  // 其次要检查当前的 BST 树是否有根节点
  // 如果没有，那么表示这是一棵新树，插入节点就是该树的根节点，那么插入这个过程就结束了；否则进行下一步
  if (this.root === null) {
    this.root = newNode;
  } else {
    // 如果待插入节点不是根节点，那么必须对 BST 进行遍历，找到合适的位置
    // 该过程类似遍历链表，用一个变量存储当前变量，一层一层遍历 BST

    // 1. 设置当前节点为根节点
    let current = this.root,
      parent;

    while (true) {
      parent = current;

      // 2. 如果待插入节点保存的数据小于当前节点，则新节点为原节点的左子节点；反之执行第 4 步
      if (value < current.value) {
        current = current.left;

        // 3. 如果当前节点的左子节点为空，则将新节点放到这个位置上，退出循环；反之继续执行下一步
        if (current === null) {
          parent.left = newNode;
          break;
        }
      } else {
        // 4. 设置新节点为原节点的右子节点
        current = current.right;

        // 5. 如果当前节点的右子节点为空，则将新节点放到这个位置上，退出循环；反之继续执行下一步
        if (current === null) {
          parent.right = newNode;
          break;
        }
      }
    }
  }
};

现在 BST 类已经初步成型，但操作仅仅限于插入节点，我们需要有遍历 BST 的能力。

遍历操作

中序遍历

BST.prototype.inOrder = function (node) {
  if (!(node === null)) {
    this.inOrder(node.left);
    console.log(node.value + ' ');
    this.inOrder(node.right);
  }
};

先序遍历

BST.prototype.preOrder = function (node) {
  if (!(node === null)) {
    console.log(node.value + ' ');
    this.preOrder(node.left);
    this.preOrder(node.right);
  }
};

后序遍历

BST.prototype.postOrder = function (node) {
  if (!(node === null)) {
    this.postOrder(node.left);
    this.postOrder(node.right);
    console.log(node.value + ' ');
  }
};

搜索操作

根据 BST 的特性，对于每个节点：

如果目标值等于节点的值，则返回节点;
如果目标值小于节点的值，则继续在左子树中搜索;
如果目标值大于节点的值，则继续在右子树中搜索。

在 BST 上查找给定值，需要比较给定值和当前节点保存的值大小，通过比较，就能确定给定值在不在当前节点，再根据 BST 的特点，向左或向右遍历。

BST.prototype.find = function (value) {
  let current = this.root;

  while (current != null) {
    if (value === current.value) {
      return current;
    } else if (value > current.value) {
      current = current.right;
    } else {
      current = current.left;
    }
  }

  return null;
};

查找最小值：

遍历左子树，直到左子树的某个节点的左子节点为 null 时，该节点保存的即为最小值。

BST.prototype.getMin = function () {
  let current = this.root;

  while (!(current.left === null)) {
    current = current.left;
  }

  return current;
};

查找最大值：

与查找最小值类似，遍历右子树，直到右子树的某个右子节点为 null 时，该节点保存的即为最大值。

BST.prototype.getMax = function () {
  let current = this.root;

  while (!(current.right === null)) {
    current = current.right;
  }

  return current;
};

查找前驱节点：

BST.prototype.predecessor = function () {};

查找后继节点：

BST.prototype.successor = function () {};

查找大于等于目标值的最小值（向上取整）

BST.prototype.ceil = function (key) {};

查找小于等于目标值的最大值（向下取整）

BST.prototype.floor = function (key) {};

删除操作

从 BST 中删除节点的操作是最为复杂的，其复杂程度取决于删除的节点位置。如果待删除的节点没有子节点，那么非常简单。如果删除包含左子节点或者右子节点，就变得稍微有些复杂。如果删除包含两个节点的节点最为复杂。

我们采用递归方法，来完成复杂的操作.

如果要删除的节点没有子节点，我们可以直接移除该节点。
如果要删除的节点有一个子节点，我们可以用其子节点作为替换。
如果要删除的节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该节点。

BST.prototype.remove = function (value) {
  this.removeNode(this.root, value);
};

BST.prototype.getSmallest = function (node) {
  if (node.left === null) {
    return node;
  } else {
    return this.getSmallest(node.left);
  }
};

BST.prototype.removeNode = function (node, value) {
  // 1. 首先判断当前节点是否包含待删除的数据值
  // 如果包含，则删除该节点
  // 如果不包含，则比较当前节点上的数据和待删除树的大小关系
  if (node === null) return null;

  if (value === node.value) {
    // 待删除节点没有子节点
    if (node.left === null && node.right === null) {
      return null;
    }

    // 待删除节点没有左子节点
    if (node.left === null) {
      return node.right;
    }

    // 待删除节点没有右子节点
    if (node.right === null) {
      return node.left;
    }

    // 待删除节点有两个子节点
    // 需要找到待删除节点左子树中的最小值
    const minNode = this.getSmallest(node.right);
    // 将右子树最小值赋值给待删除节点
    node.value = minNode.value;
    // 删除右子树刚才找到的最小值的节点
    node.right = removeNode(node.right, minNode.value);

    return node;
  } else if (value < node.value) {
    // 如果待删除的数据值小于当前节点的数据，则移至当前节点的左子节点继续比较
    node.left = this.removeNode(node.left, value);

    return node;
  } else {
    // 如果待删除的数据值大于当前节点的数据，则移至当前节点的右子节点继续比较
    node.right = this.remove(node.right, value);

    return node;
  }
};

特性

局限性

同样的数据，不同的插入顺序，树的结果是不一样的，如下图所示：

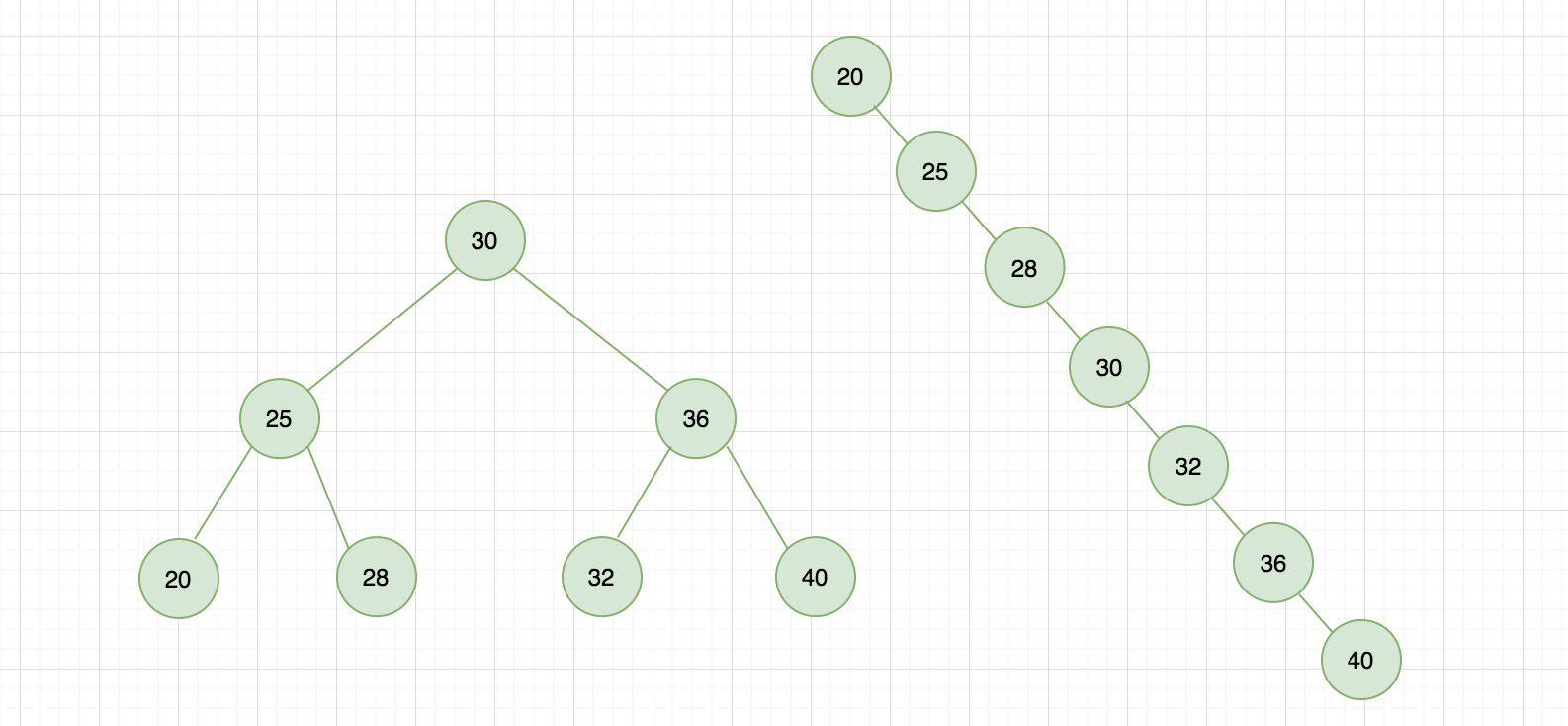
这就是二叉搜索树存在的问题，它可能是极端的，并不总是像左侧永远是一个平衡的二叉树，如果我顺序化插入树的形状就如右侧所示，会退化成一个链表，试想如果我需要查找节点 40，在上图所示的树形中需要遍历完所有节点，相比于左侧时间性能会消耗一倍。

为了解决这一问题，可能需要一种平衡的二叉搜索树，常用的实现方法有红黑树、AVL 树等。

高度平衡的二叉搜索树

树结构中的常见用语：
节点的深度：从树的根节点到该节点的边数
节点的高度：该节点和叶子之间最长路径上的边数
树的高度：其根节点的高度

一个高度平衡的二叉搜索树（平衡二叉搜索树）是在插入和删除任何节点之后，可以自动保持其高度最小。也就是说，有 N 个节点的平衡二叉搜索树，它的高度是 logN。并且，每个节点的两个子树的高度不会相差超过 1。

为什么是 log n 呢？
一个高度为 h 的二叉树 2^0 + 2^1 + ... + 2^h = 2^(h+1) -1
换言之，一个有 N 个节点，且高度为 h 的二叉树：N <= 2^(h+1) - 1
所以：h >= [log2 N]

下面是一个普通二叉搜索树和一个高度平衡的二叉搜索树的例子:

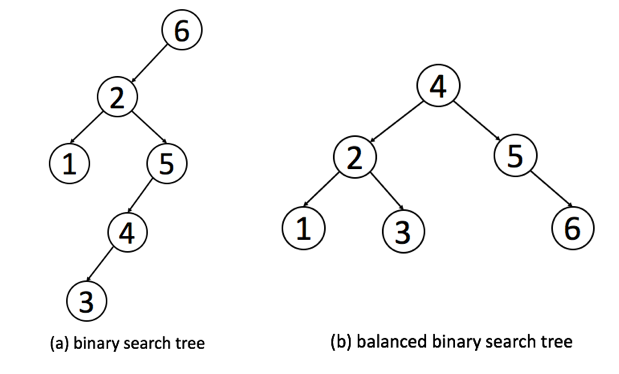
根据定义，我们可以判断出一个二叉搜索树是否是高度平衡的 (平衡二叉树)。

正如我们之前提到的, 一个有 N 个节点的平衡二搜索叉树的高度总是 logN。因此，我们可以计算 节点总数 和 树的高度，以确定这个二叉搜索树是否为高度平衡的。

同样，在定义中，我们提到了高度平衡的二叉树一个特性: 每个节点的两个子树的深度不会相差超过 1。我们也可以根据这个性质，递归地验证树。

必要性

为什么需要用到高度平衡的二叉搜索树?

我们已经介绍过了二叉树及其相关操作, 包括搜索、插入、删除。当分析这些操作的时间复杂度时，我们需要注意的是树的高度是十分重要的考量因素。以搜索操作为例，如果二叉搜索树的高度为 h，则时间复杂度为 O(h)。二叉搜索树的高度的确很重要。

所以，我们来讨论一下树的节点总数 N 和高度 h 之间的关系。对于一个平衡二叉搜索树, 我们已经在前文中提过 h >= [log2 N]。但对于一个普通的二叉搜索树，在最坏的情况下, 它可以退化成一个链。

因此，具有 N 个节点的二叉搜索树的高度在 logN 到 N 区间变化。也就是说，搜索操作的时间复杂度可以从 logN 变化到 N。这是一个巨大的性能差异。

所以说，高度平衡的二叉搜索树对提高性能起着重要作用。

实现方式

有许多不同的方法可以实现。尽管这些实现方法的细节有所不同，但他们有相同的目标:

采用的数据结构应该满足二分查找属性和高度平衡属性。
采用的数据结构应该支持二叉搜索树的基本操作，包括在 O(logN) 时间内的搜索、插入和删除，即使在最坏的情况下也是如此。

我们提供了一个常见的的高度平衡二叉树列表供您参考：

红黑树
AVL 树
伸展树（Splay Tree）
树堆

实际应用

高度平衡的二叉搜索树在实际中被广泛使用，因为它可以在 O(logN) 时间复杂度内执行所有搜索、插入和删除操作。

平衡二叉搜索树的概念经常运用在 Set 和 Map 中。Set 和 Map 的原理相似。我们将在下文中重点讨论 Set 这个数据结构。

Set（集合）是另一种数据结构，它可以存储大量 key（键）而不需要任何特定的顺序或任何重复的元素。它应该支持的基本操作是将新元素插入到 Set 中，并检查元素是否存在于其中。

通常，有两种最广泛使用的集合：散列集合（Hash Set）和树集合（Tree Set）。

树集合, Java 中的 Treeset 或者 C++ 中的 set，是由高度平衡的二叉搜索树实现的。因此，搜索、插入和删除的时间复杂度都是 O(logN)。

散列集合, Java 中的 HashSet 或者 C++中的 unordered_set，是由哈希实现的, 但是平衡二叉搜索树也起到了至关重要的作用。当存在具有相同哈希键的元素过多时，将花费 O(N) 时间复杂度来查找特定元素，其中 N 是具有相同哈希键的元素的数量。通常情况下，使用高度平衡的二叉搜索树将把时间复杂度从 O(N) 改善到 O(logN)。

哈希集和树集之间的本质区别在于树集中的键是有序的。

参考资料：

Data Structure and Algorithms Guidebook