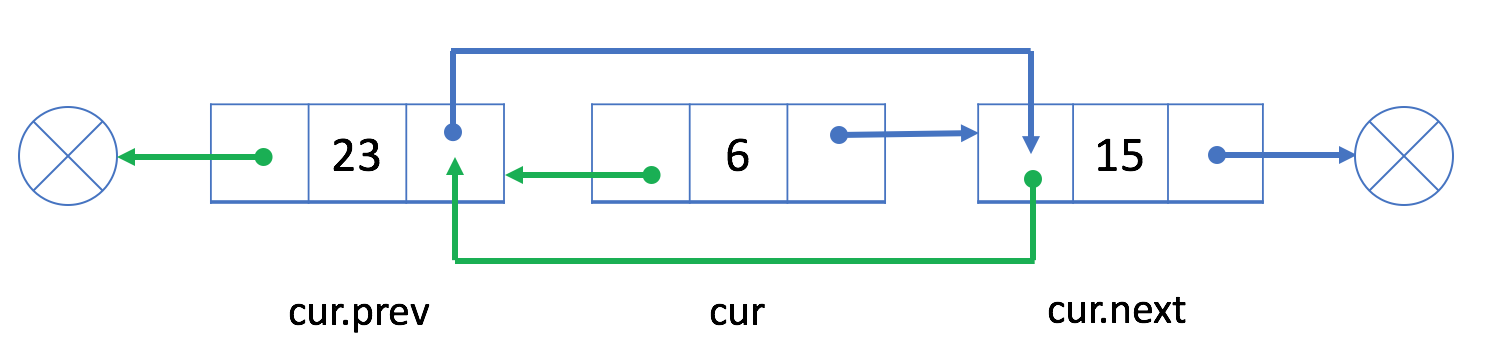
双链表

双链表与单链表类似的方式工作，但还有一个引用字段，称为 prev 字段。有了这个额外的字段，您就能够知道当前结点的前一个结点。

绿色箭头表示我们的 prev 字段是如何工作的。

结点结构

下面是双链表中结点结构的典型定义：

// Definition for doubly-linked list.
class DoublyListNode {
    int val;
    DoublyListNode next, prev;
    DoublyListNode(int x) {val = x;}
}

与单链接列表类似，我们将使用 头结点 来表示整个列表。

基本操作

与单链表类似，我们将介绍在双链表中如何访问数据、插入新结点或删除现有结点。

我们可以与单链表相同的方式访问数据：

1. 我们不能在常量级的时间内 访问随机位置。
2. 我们必须从头部遍历才能得到我们想要的第一个结点。
3. 在最坏的情况下，时间复杂度将是 O(N)，其中 N 是链表的长度。

对于添加和删除，会稍微复杂一些，因为我们还需要处理 prev 字段。

添加操作

如果我们想在现有的结点 prev 之后插入一个新的结点 cur，我们可以将此过程分为两个步骤：

1. 链接 cur 与 prev 和 next，其中 next 是 prev 原始的下一个节点；

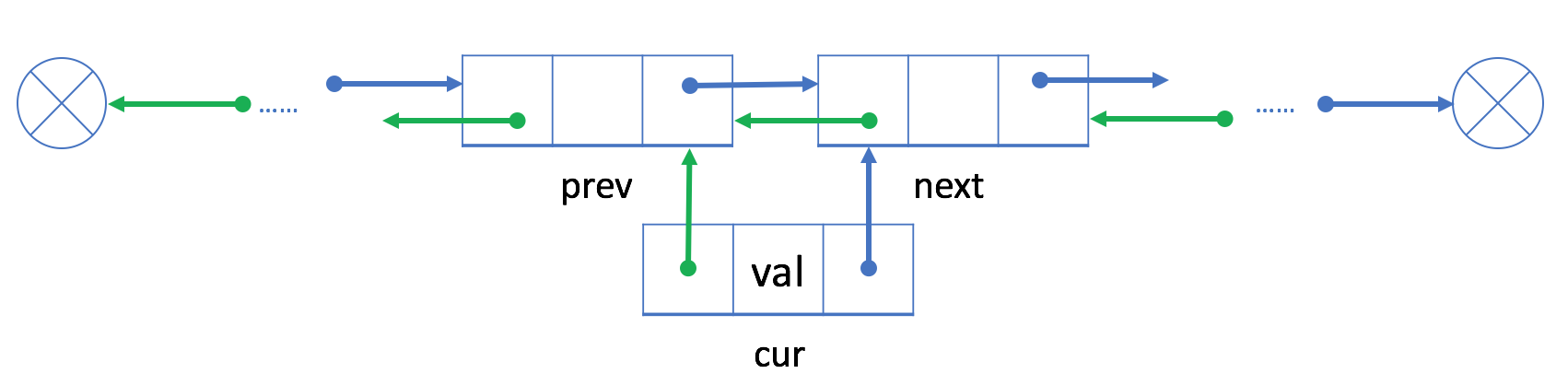
2. 用 cur 重新链接 prev 和 next。

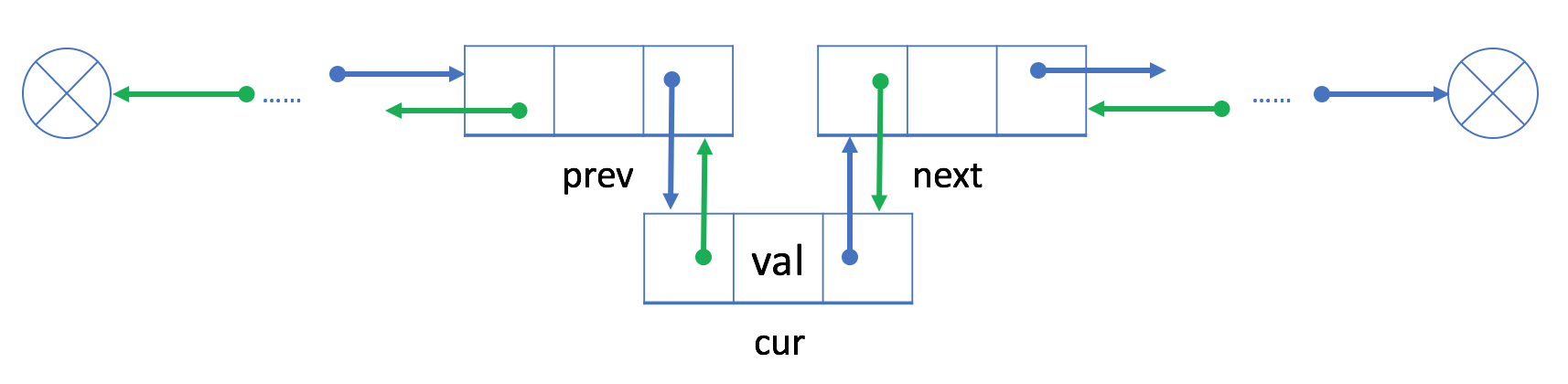
与单链表类似，添加操作的时间和空间复杂度都是 O(1)。

示例

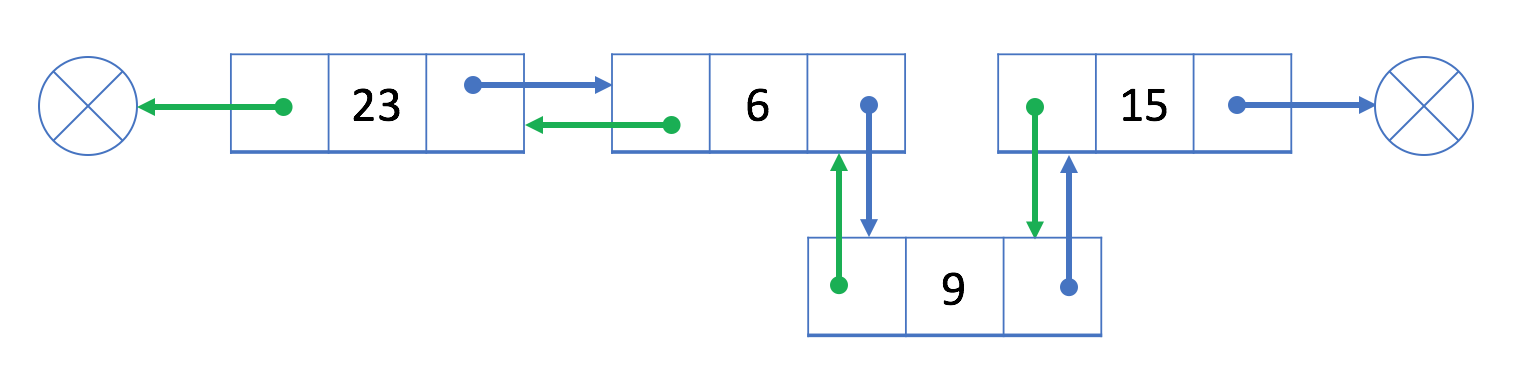
让我们在现有结点 6 之后添加一个新结点 9：

1. 链接 cur（结点 9）与 prev（结点 6）和 next（结点 15）

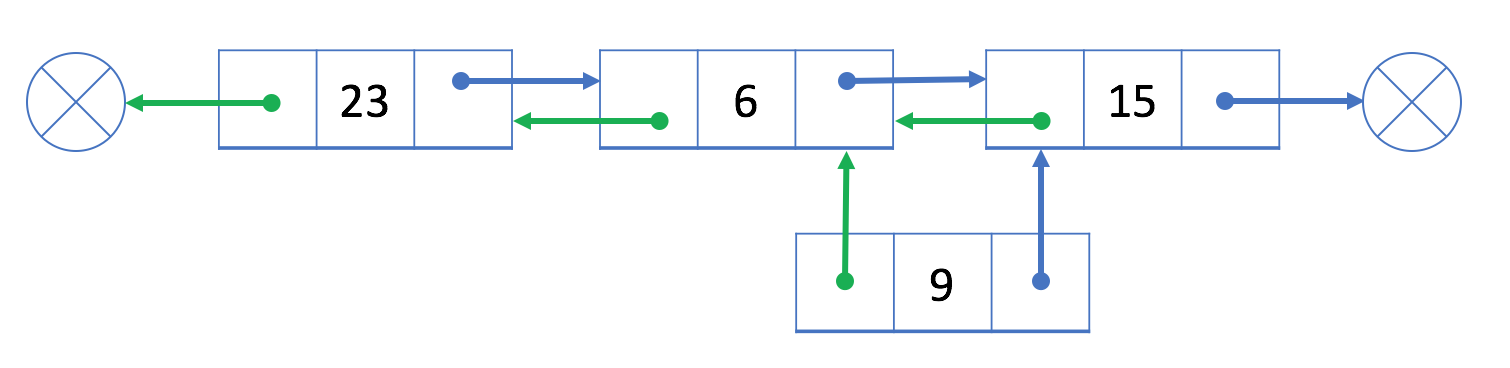
2. 用 cur（结点 9）重新链接 prev（结点 6）和 next（结点 15）

删除操作

如果我们想从双链表中删除一个现有的结点 cur，我们可以简单地将它的前一个结点 prev 与下一个结点 next 链接起来。

与单链表不同，使用 prev 字段可以很容易地在常量时间内获得前一个结点。

因为我们不再需要遍历链表来获取前一个结点，所以时间和空间复杂度都是 O(1)。

示例

我们的目标是从双链表中删除结点 6。

因此，我们将它的前一个结点 23 和下一个结点 15 链接起来：