哈希表
哈希表 是一种使用 哈希函数 组织数据,以支持快速插入和搜索的数据结构。
有两种不同类型的哈希表:哈希集合和哈希映射。
哈希集合是集合数据结构的实现之一,用于存储非重复值。哈希映射是映射数据结构的实现之一,用于存储(key, value)键值对。
在 标准模板库 的帮助下,哈希表是 易于使用的。大多数常见语言(如 Java,C ++ 和 Python)都支持哈希集合和哈希映射。
通过选择合适的哈希函数,哈希表可以在插入和搜索方面实现 出色的性能。
原理
正如我们在介绍中提到的,哈希表 是一种数据结构,它使用哈希函数组织数据,以支持 快速插入和搜索。在本文中,我们将简要说明哈希表的原理。
哈希表的关键思想是使用 哈希函数 将键映射到存储桶。更确切地说,
- 当我们插入一个新的键时,哈希函数将决定该键应该分配到哪个桶中,并将该键存储在相应的桶中;
- 当我们想要搜索一个键时,哈希表将使用相同的哈希函数来查找对应的桶,并只在特定的桶中进行搜索。
🌰 示例:
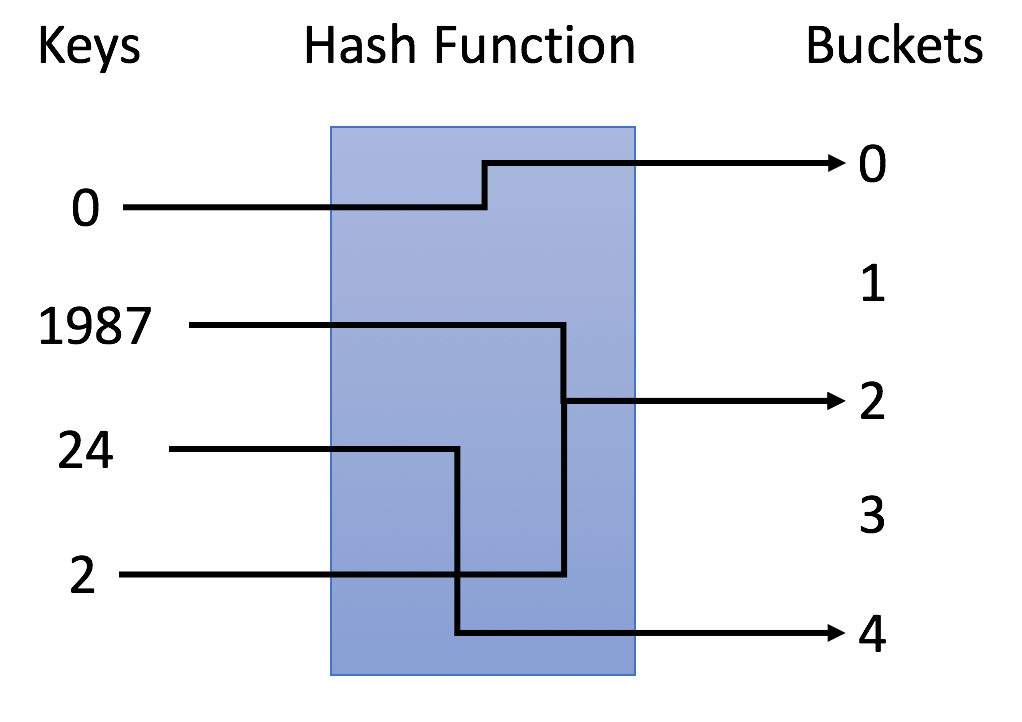
在示例中,我们使用 y = x % 5 作为哈希函数。让我们使用这个例子来完成插入和搜索策略:
- 插入:我们通过哈希函数解析键,将它们映射到相应的桶中。
- 例如,1987 分配给桶 2,而 24 分配给桶 4。
- 搜索:我们通过相同的哈希函数解析键,并仅在特定存储桶中搜索。
- 如果我们搜索 1987,我们将使用相同的哈希函数将 1987 映射到 2。因此我们在桶 2 中搜索,我们在那个桶中成功找到了 1987。
- 例如,如果我们搜索 23,将映射 23 到 3,并在桶 3 中搜索。我们发现 23 不在桶 3 中,这意味着 23 不在哈希表中。
插入 和 搜索 是哈希表中的两个基本操作。
设计关键
在设计哈希表时,你应该注意两个基本因素。
哈希函数
哈希函数是哈希表中最重要的组件,该哈希表用于将键映射到特定的桶。在上一篇文章中的示例中,我们使用 y = x % 5 作为散列函数,其中 x 是键值,y 是分配的桶的索引。
散列函数将取决于 键值的范围 和 桶的数量。
下面是一些哈希函数的示例:
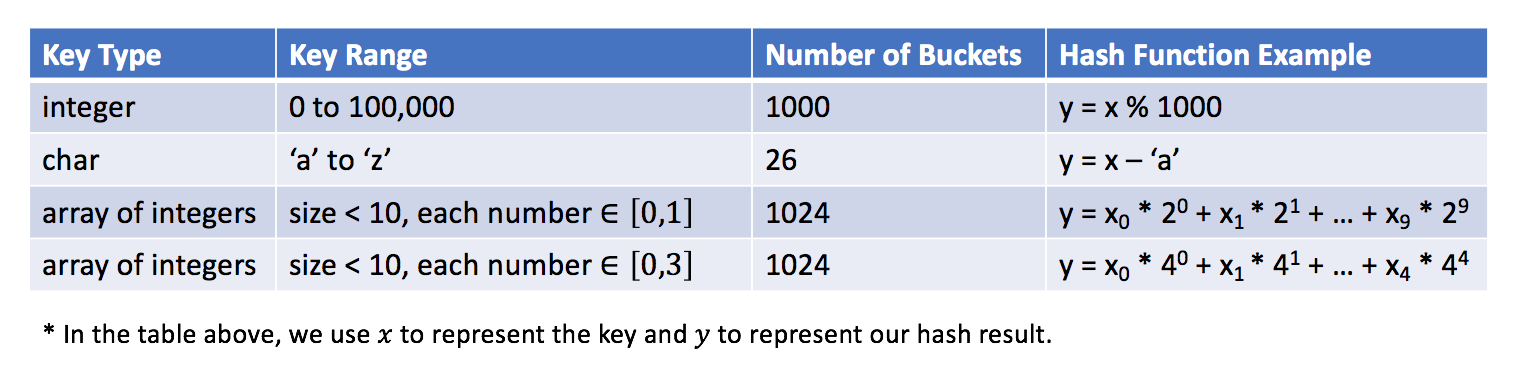
哈希函数的设计是一个开放的问题。其思想是尽可能将键分配到桶中,理想情况下,完美的哈希函数将是键和桶之间的一对一映射。然而,在大多数情况下,哈希函数并不完美,它需要在桶的数量和桶的容量之间进行权衡。
冲突解决
理想情况下,如果我们的哈希函数是完美的一对一映射,我们将不需要处理冲突。不幸的是,在大多数情况下,冲突几乎是不可避免的。例如,在我们之前的哈希函数 y = x % 5 中,1987 和 2 都分配给了桶 2,这是一个冲突。
冲突解决算法应该解决以下几个问题:
- 如何组织在同一个桶中的值?
- 如果为同一个桶分配了太多的值,该怎么办?
- 如何在特定的桶中搜索目标值?
根据我们的哈希函数,这些问题与 桶的容量 和可能映射到 同一个桶 的 键的数目 有关。
让我们假设存储最大键数的桶有 N 个键。
通常,如果 N 是常数且很小,我们可以简单地使用一个数组将键存储在同一个桶中。如果 N 是可变的或很大,我们可能需要使用 高度平衡的二叉树 来代替。
实际应用
哈希集合
哈希集 是集合的实现之一,它是一种存储 不重复值 的数据结构。
哈希映射
哈希映射 是用于存储 (key, value) 键值对的一种实现。
设计键
在以前的问题中,键的选择相对简单。不幸的是,有时你必须考虑在使用哈希表时设计合适的键。
解决方案:
实际上,设计关键 是在原始信息和哈希映射使用的实际键之间 建立映射关系。设计键时,需要保证:
- 属于同一组的所有值都将映射到同一组中。
- 需要分成不同组的值不会映射到同一组。
此过程类似于设计哈希函数,但这是一个本质区别。哈希函数满足第一个规则但 可能不满足第二个规则。但是你的映射函数应该满足它们。
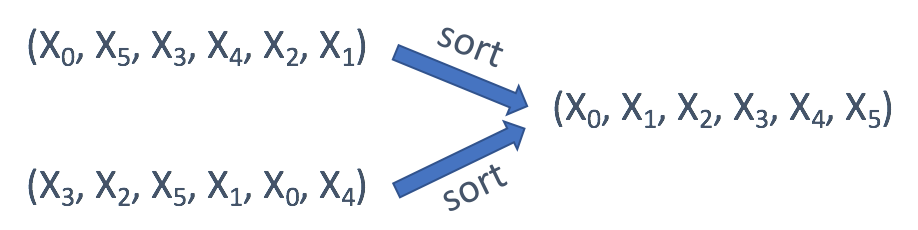
在上面的示例中,我们的映射策略可以是:对字符串进行排序并使用排序后的字符串作为键。也就是说,“eat” 和 “ate” 都将映射到 “aet”。
这里有一些为你准备的关于如何设计键的建议。
- 当字符串 / 数组中每个元素的顺序不重要时,可以使用
排序后的字符串 / 数组作为键。
- 如果只关心每个值的偏移量,通常是第一个值的偏移量,则可以使用
偏移量作为键。
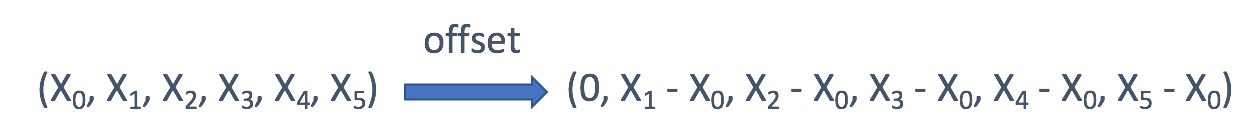
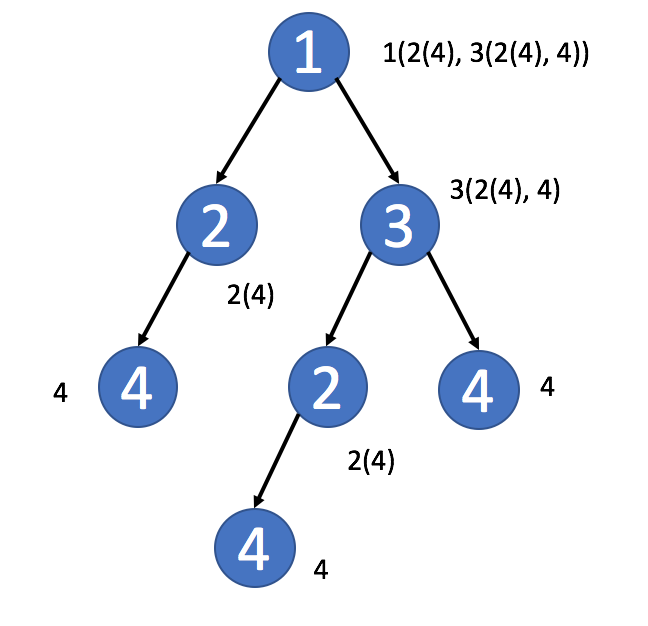
- 在树中,你有时可能会希望直接使用
TreeNode作为键。 但在大多数情况下,采用子树的序列化表述可能是一个更好的主意。
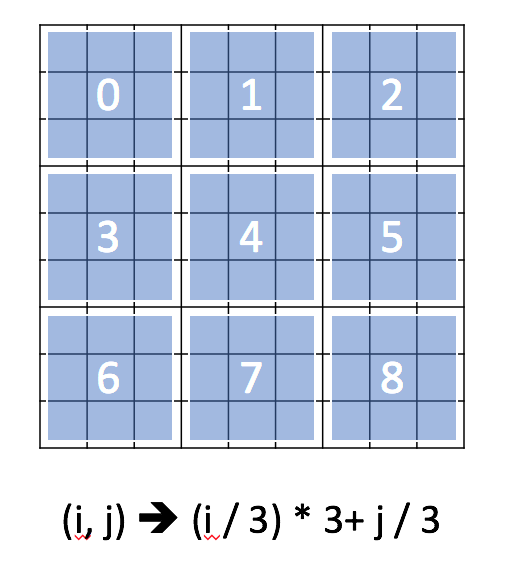
- 在矩阵中,你可能希望使用
行索引或列索引作为键。
- 在数独中,可以将行索引和列索引组合来标识此元素属于哪个
块。
- 有时,在矩阵中,您可能希望将值聚合在
同一对角线中。