计数排序

计数排序（Counting Sort）使用一个额外的数组 counter，其中第 i 个元素是待排序数组 arr 中值等于 i 的元素的个数。

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是 有确定范围的整数。

用来计数的数组 counter 的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上 1），然后进行分配、收集处理：

分配：扫描一遍原始数组，以当前值 -minValue 作为下标，将该下标的计数器增 1。
收集：扫描一遍计数器数组，按顺序把值收集起来。

算法原理

找出待排序的数组中最大和最小的元素
统计数组中每个值为 i 的元素出现的次数，存入数组 counter 的第 i 项
对所有的计数累加（从 counter 中的第一个元素开始，每一项和前一项相加）
反向填充目标数组：将每个元素 i 放在新数组的第 counter(i) 项，每放一个元素就将 counter(i) 减去 1

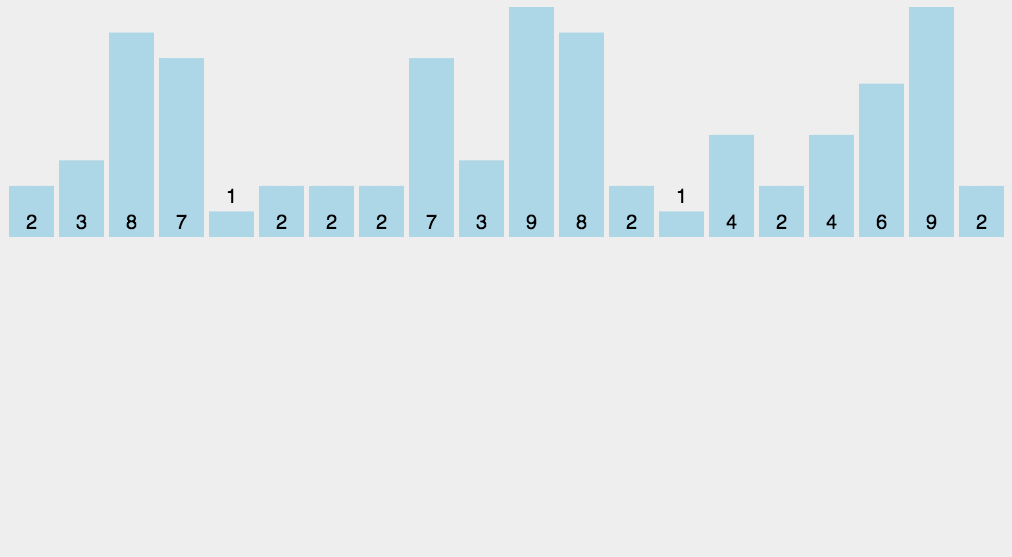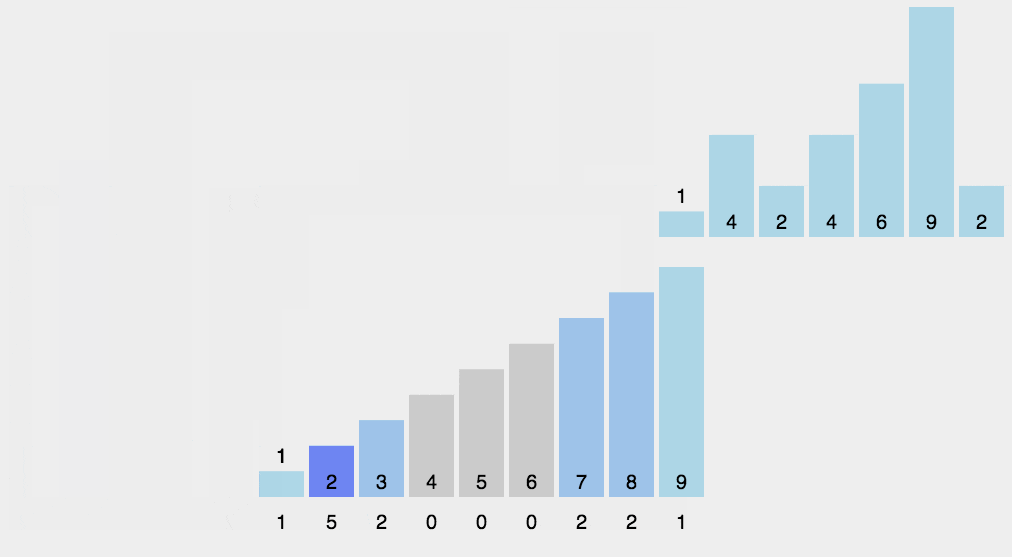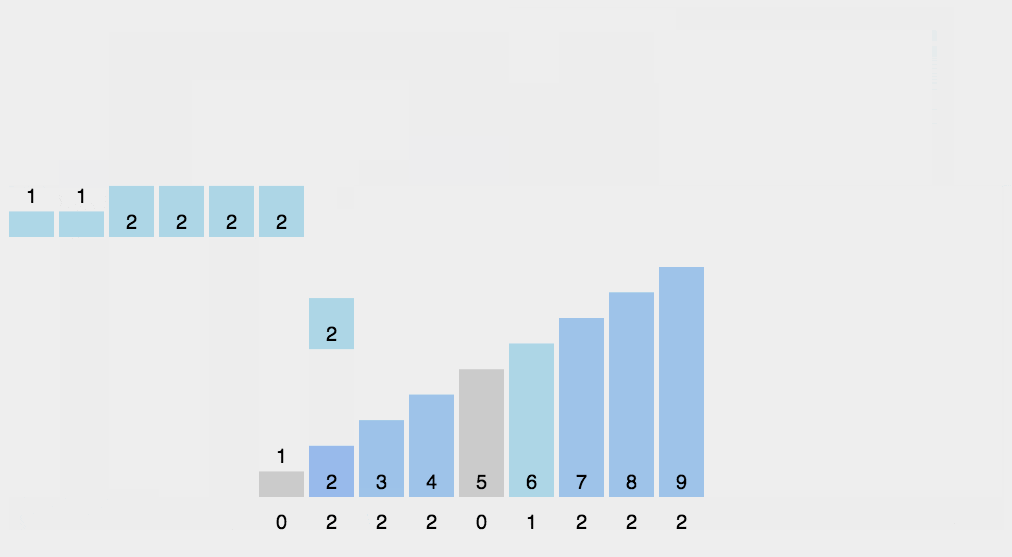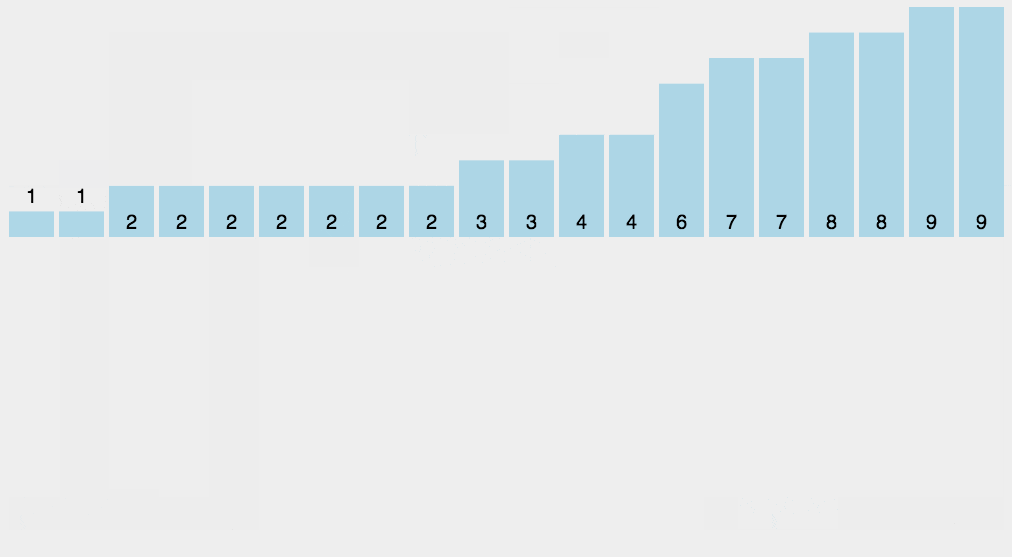
适用于量大但是范围小的场景。

算法实现

const countingSort = function(arr) {
  var len = arr.length,
    // 计数数组
    counter = [],
    // 放排序后值的数组
    sorted = [],
    min = (max = arr[0]);

  // 找出待排序数组中最大和最小的元素
  for (var i = 0; i < len; i++) {
    min = min <= arr[i] ? min : arr[i];
    max = max >= arr[i] ? max : arr[i];

    // 统计数组中元素出现的次数
    counter[arr[i]] = counter[arr[i]] ? counter[arr[i]] + 1 : 1;
  }

  for (var j = min; j < max; j++) {
    counter[j + 1] = (counter[j + 1] || 0) + (counter[j] || 0);
  }

  for (var k = len - 1; k >= 0; k--) {
    sorted[counter[arr[k]] - 1] = arr[k];
    counter[arr[k]]--;
  }

  return sorted;
};

Data Structure and Algorithms Guidebook

计数排序

算法原理

算法实现