KMP 算法

Knuth-Morris-Pratt 字符串查找算法，简称为 KMP 算法，常用于在一个文本串 S 内查找一个模式串 P 的出现位置。

KMP 算法相比于 BF 算法的优点在于能动态地调整每次往后移动的距离，而 BF 算法则每次只能 +1。

算法推倒过程

KMP 算法的核心，是一个被称为部分匹配表（Partial Match Table）的数组。

前缀和后缀

以字符串 abababca 为例：

字符 `char`	索引 `index`	值 `value`
`a`	0	0
`b`	1	0
`a`	2	1
`b`	3	2
`a`	4	3
`b`	5	4
`c`	6	0
`a`	7	1

前缀：指除了最后一个字符外，一个字符串的全部头部组合。例如，Harry 的前缀包括 { "H", "Ha", "Har", "Harr" }，我们把所有前缀组成的集合，称为字符串的前缀集合
后缀：指除了第一个字符外，一个字符串的全部尾部组合。例如，Potter 的后缀包括 { "otter", "tter", "er", "r" }，然后把所有后缀组成的集合，称为字符串的后缀集合。

需要注意的是，字符串本身并不是自己的后缀。

有了这个定义，我们就能说明 PMT 中值的意义。PMT 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。

例如，对于 "aba"，它的前缀集合为 { "a", "ab" }，后缀集合为 { "ba", "a" }。两个集合的交集为 { "a" }，那么长度最长的元素就是字符串 "a" 了，长度为1，所以对于 "aba" 而言，它在 PMT 表中对应的值就是 1。

再比如，对于字符串 "ababa"，它的前缀集合为 { "a", "ab", "aba", "abab" }，它的后缀集合为 { "baba", "aba", "ba", "a" }，两个集合的交集为 { "a", "aba" }，其中最长的元素为 "aba"，长度为3。

部分匹配表的运用

解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么。

要在文本串 "ababababca" 中查找模式串 "abababca"。如果在 j 处字符不匹配，那么由于上文所说的模式串 PMT 的性质，文本串中 i 指针之前的 PMT[j - 1] 位就一定与模式字符串的第 0 位至第 PMT[j − 1] 位是相同的。这是因为文本串在 i 位失配，也就意味着文本串从 i − j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。而我们上面也解释了，模式字符串从 0 到 j − 1 ，在这个例子中就是 "ababab"，其前缀集合与后缀集合的交集的最长元素为 "abab"，长度为 4。所以就可以断言，文本串中 i 指针之前的 4 位一定与模式字符串的第 0 位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持 i 指针不动，然后将 j 指针指向模式字符串的 PMT[j − 1] 位即可。

简言之，以图中的例子来说，在 i 处失配，那么文本串和模式字符串的前边 6 位就是相同的。又因为模式字符串的前 6 位，它的前 4 位前缀和后 4 位后缀是相同的，所以我们推知主字符串 i 之前的 4 位和模式字符串开头的 4 位是相同的。就是图中的灰色部分。那这部分就不用再比较了。

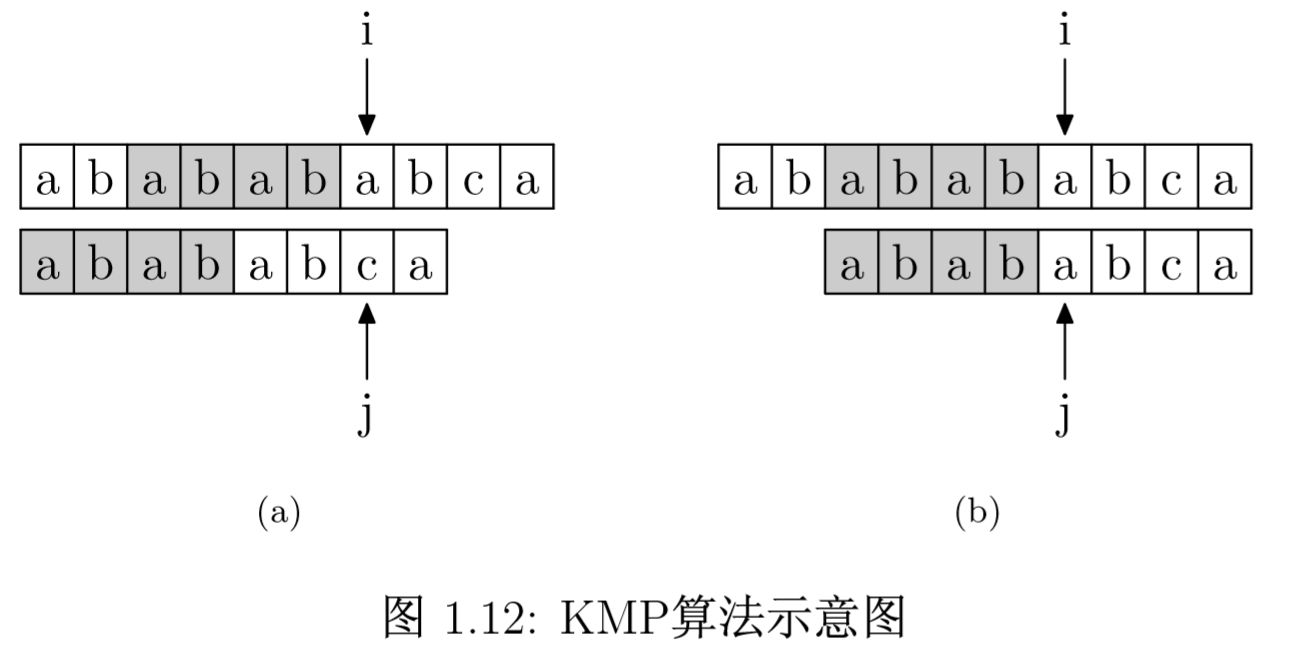
有了上面的思路，我们就可以使用 PMT 加速字符串的查找了。我们看到如果是在 j 位失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值。

算法实现

终极版本

前缀的末尾是 arr.length - 1，后缀的末尾是 1。

// 用 table[i] 作为子串 0..i 的最长前缀的长度构造一个表
function longestPrefix(str) {
  // 创建一个大小等于模式串长度的表（使用数组表示）
  // table[i] 将存储子字符串 str[0..i] 的最长前缀的前缀
  const table = new Array(str.length);
  let maxPrefix = 0;

  // 子字符串 str[0] 的最长前缀具有长度
  table[0] = 0;

  // 对于下面的子串，我们有两种情况
  for (let i = 1; i < str.length; i++) {
    // 情况 1: 当前字符不匹配最长前缀的最后一个字符
    while (maxPrefix > 0 && str.charAt(i) !== str.charAt(maxPrefix)) {
      // 如果是这种情况，我们必须回溯，并试图找到一个字符，将等于当前字符
      // 如果我们到达 0，那么我们就找不到匹配的字符
      maxPrefix = table[maxPrefix - 1];
    }

    // 情况 2:最长前缀的最后一个字符与 str 中的当前字符匹配
    if (str.charAt(maxPrefix) === str.charAt(i)) {
      // 如果是这种情况，我们知道在位置 i 的最长前缀还有一个字符
      // 例如，考虑 `-` 不是集合 `[a-c]` 中包含的任何字符
      // str = abc----abc
      // 假设 i 将会是字符 c 在字符串 str 中的最后的索引
      // 那么 maxPrefix 将会是 2（字符串 str 中第一个字符 `c`）
      // maxPrefix 将会是 3
      maxPrefix++;
      // 所以 table[9] 的最长前后缀是 3
    }

    table[i] = maxPrefix;
  }

  return table;
}

// 查找 str 中所有匹配模式串的字符串
// 该算法基于 Knuth—Morris-Pratt 算法，它的优化在于它与 O(n) 复杂度匹配
function kmpMatching(str, pattern) {
  const next = longestPrefix(pattern);
  let matches = [];

  // 文本串中的索引
  let i = 0;
  // 模式串中的索引
  let j = 0;

  while (i < str.length) {
    // 情况 1: S[i] === P[j]，因此我们分别将 S 和 P 的索引向下个索引移动
    if (str.charAt(i) === pattern.charAt(i)) {
      i++;
      j++;
    }

    // 情况 2: j 与模式串长度相等
    // 这表示我们到达了模式串的末端，也就是说我们找到了匹配的字符串
    if (j === pattern.length) {
      matches.push(i - j);
      // 下面我们必须更新 `j`，因为我们想匹配多次
      // 我们可以跳转到目前已知的最长前缀的最后一个字符，而不是更新到 `j = 0`
      // `j - 1` 表示模式串最后字符，因为 `j` 事实上就是 `P.length`
      // 例如：
      // S =  a b a b d e
      // P = `a b`a b
      // 我们会跳转到 `a b` 并且我们会在下次迭代中比较 `d`
      // a b a b `d` e
      //     a b `a` b
      j = next[j - 1];
    }
    // 情况 3:
    // S[i] !== P[j] 表示失配
    else if (str.charAt(i) !== pattern.charAt(j)) {
      // 如果我们至少找到了一个共同的字符，请执行与情况 2 中相同的操作
      if (j !== 0) {
        j = next[j - 1];
      } else {
        // 否则，j = 0，我们可以移动到下个字符 S[i + 1]
        i++;
      }
    }
  }

  return matches;
}

参考资料：