Data Structure and Algorithms Guidebook

数据结构与算法完全知识体系

股票买卖问题

  1. 买卖股票的最佳时机（LeetCode 121）
  2. 买卖股票的最佳时机 II（LeetCode 122）
  3. 买卖股票的最佳时机 III（LeetCode 123）
  4. 买卖股票的最佳时机 IV（LeetCode 309）
  5. 最佳买卖股票时机含冷冻期（LeetCode 188）
  6. 买卖股票的最佳时机含手续费（LeetCode 714）

动态规划基本方程：

  1. 状态转移方程
  2. 最优值函数
  3. 边界条件

穷举框架

递归其实是符合我们思考的逻辑的，一步步推进，遇到无法解决的就丢给递归，一不小心就做出来了，可读性还很好。缺点就是一旦出错，你也不容易找到错误出现的原因。比如上篇文章的递归解法，肯定还有计算冗余，但确实不容易找到。

而这里，我们不用递归思想进行穷举，而是利用 状态 进行穷举。我们具体到每一天，看看总共有几种可能的 状态，再找出每个 状态 对应的 选择。我们要穷举所有 状态，穷举的目的是根据对应的 选择 更新状态。听起来抽象，你只要记住 状态 和 选择 两个词就行，下面实操一下就很容易明白了。

for (let condition1 of collection1) {
  for (let condition2 of collection2) {
    for ...
      // pick 相当于 择优
      dp[condition1][condition2] = pick(condition1, condition2)
  }
}

比如说 买卖股票的最佳时机，每天都有三种 选择：买入、卖出 和 无操作，我们用 buy、sell 和 rest 表示这三种选择。

但问题是，并不是每天都可以任一选择这三种选择，因为 sell 必须在 buy 之后，buy 必须在 sell 之后。那么 rest 操作还应该分两种状态：

  • 一种是 buy 之后的 rest（持有了股票）
  • 一种是 sell 之后的 rest（没有持有股票）

而且别忘了，我们还有交易次数 的限制，就是说你 buy 还只能在 k > 0 的前提下操作。

穷举法，这个问题的状态有三个：

  1. 天数
  2. 允许交易的最大次数
  3. 当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）

然后我们用一个三维数组就可以装下几种状态的全部组合：

dp[i][k][0 or 1]
0 <= i <= n - 1
1 <= k <= K


n 为天数，大 K 最多交易数
此问题共 n * k * 2 种交易状态，全部穷举就能搞定


for (0 <= i < n) {
  for (1 <= k <= K) {
    for (let s in {0, 1}) {
      dp[i][k][s] = max(buy, sell, rest)
    }
  }
}

用自然语言描述状态含义，例如：

  • dp[3][2][1]：今天是第三天，我现在手上持有股票，至今最多进行 2 次交易
  • dp[2][3][0]：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易

我们想求的最终答案是 dp[n - 1][k][0]，即最后一天，最多允许 次交易，最多获得多少利润。可能会奇怪为何不是 dp[n - 1][k][1]。这是因为 [1] 代表手上还持有股票，[0] 表示手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。

记住如何解释 状态，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。

状态转移框架

现在，我们已经完成了 状态 的穷举，我们开始思考每种 状态 有哪些 选择，应该如何更新 状态。只看 持有状态，可以画个状态转移图。

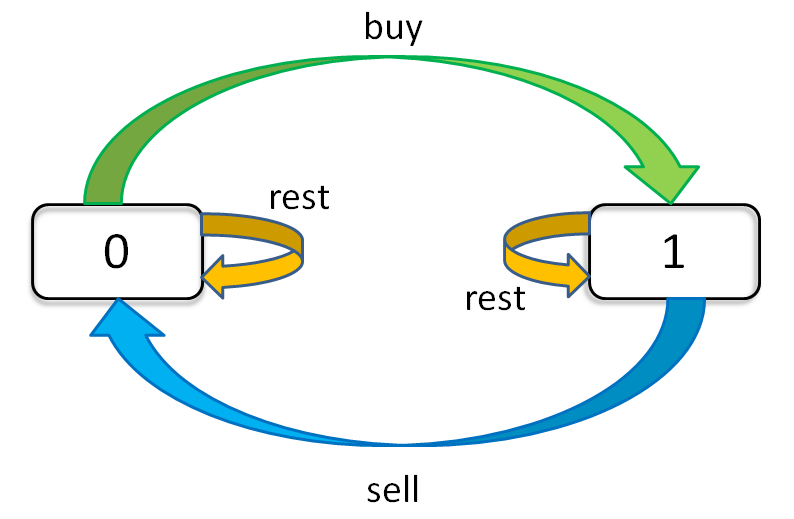
状态转移框架

根据这个图写出状态转移方程：

dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i])
              max( <rest>, <sell> )

如果今天没有持有股票，有两种可能：

  • 要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有
  • 要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
              max( <rest>, <sell>)

如果今天持有股票，有两种可能：

  • 要么我昨天就持有股票，然后今天选择 rest，所以我今天依然持有股票
  • 要么我昨天没有持有股票，但今天我选择 buy，所以今天我就持有股票了

如果 buy，就要从利润中减去 ，如果 sell，就要给利润增加 。

今天的最大利润就是这两种可能选择中较大的那个，而且注意 k 的限制，我们在选择 buy 的时候，把 k 减少了 1，很好理解吧，当然你也可以在 sell 的时候减 1，一样的。

现在，我们已经完成了动态规划中最难的一步：状态转移方程。如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就醒了。不过还差最后一点点，就是定义 Base Case，即最简单的情况。

// 因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0
dp[i - 1][k][0] = 0;


// 还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能
dp[-1][k][1] = -Infinity;


// 因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0
dp[i][0][0] = 0;


// 不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能
dp[i][0][1] = -Infinity;

把上面的状态转移方程总结一下：

// 最简单的情况
dp[-1][k][0] = dp[i][0][0] = 0;
dp[-1][k][1] = dp[i][0][1] = -Infinity;


dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);

秒杀题目

通用解法

const maxProfit = function (k, prices, fee, m) {
  if (k === 0 || prices === null || prices.length < 2) return 0;


  const len = prices.length;


  if (k > len >> 1) {
  }


  let profit = [];


  for (let i = 0; i < len; i++) {
    for (let j = 0; j < k + 1; j++) {
      if (i === 0 || j === 0) {
      }


      if (i < m + 1) {
      }


      profit[i][j][0] = Math.max(profit[i - 1][j][0], profit[i - 1][j][1] + prices[i] - fee);
      profit[i][j][1] = Math.max(profit[i - 1][j][1], profit[i - (m + 1)][0] - prices[i]);
    }
  }


  return profit[len - 1][k][0];
};
Edit this doc on GitHub2/21/2022 13:38:33