桶排序

桶排序（Bucket Sort）是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

为了使桶排序更加高效，我们需要做到这两点：

在额外空间充足的情况下，尽量增大桶的数量
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

算法原理

设置一个定量的数组当作空桶子
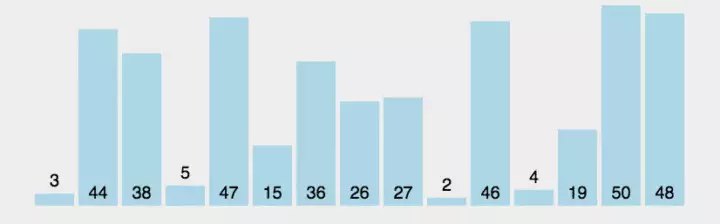
寻访序列，并且把项目一个一个放到对应的桶子去
对每个不是空的桶子进行排序
从不是空的桶子里把项目再放回原来的序列中

算法分析

平均时间复杂度：O(n + k)
最佳时间复杂度：O(n + k)
最差时间复杂度：O(n ^ 2)
空间复杂度：O(n * k)
稳定性：稳定

桶排序最好情况下使用线性时间 O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为 O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

算法实现

function bucketSort(arr, num) {
  if (arr.length <= 1) {
    return arr;
  }

  var len = arr.length,
    buckets = [],
    result = [],
    min = (max = arr[0]),
    regex = '/^[1-9]+[0-9]*$/',
    space,
    n = 0;

  num = num || (num > 1 && regex.test(num) ? num : 10);

  for (var i = 1; i < len; i++) {
    min = min <= arr[i] ? min : arr[i];
    max = max >= arr[i] ? max : arr[i];
  }

  space = (max - min + 1) / num;

  for (var j = 0; j < len; j++) {
    var index = Math.floor((arr[j] - min) / space);
    if (buckets[index]) {
      //  非空桶，插入排序
      var k = buckets[index].length - 1;
      while (k >= 0 && buckets[index][k] > arr[j]) {
        buckets[index][k + 1] = buckets[index][k];
        k--;
      }
      buckets[index][k + 1] = arr[j];
    } else {
      //空桶，初始化
      buckets[index] = [];
      buckets[index].push(arr[j]);
    }
  }

  while (n < num) {
    result = result.concat(buckets[n]);
    n++;
  }

  return result;
}

Data Structure and Algorithms Guidebook

桶排序

算法原理

算法分析

算法实现